Page 318 - Physical Principles of Sedimentary Basin Analysis

300 Flexure of the lithosphere

a compressive force will not have much impact on nearly plane plates. The same applies
for a plate deflected with large wave numbers (small wavelengths). The critical force F c
reaches a minimum for a wave number between the two limiting regimes of very short or
very long wave numbers. The wave number for the minimum critical force is found by
solving dF c /k = 0, which gives

g D

1/4
1/4
k min = or λ min = 2π . (9.77)
D g
The least possible critical force is

F c,min = F c (k min ) = 2(D g) 1/2 . (9.78)
We see that both the wavelength λ min and the critical force F c,min depend on the coefficient
3
2
of flexural rigidity D = Eh /(12(1 − ν )), which again depends on the plate thickness h.
The force F c,min can be related to the corresponding compressive stress by
σ c,min = F c,min /h. (9.79)

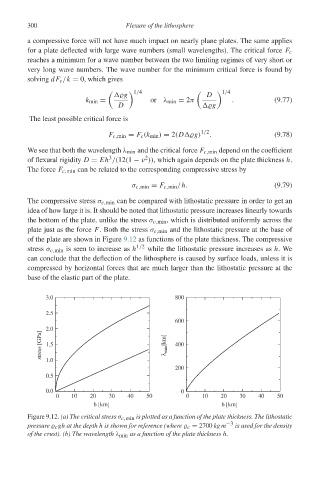
The compressive stress σ c,min can be compared with lithostatic pressure in order to get an
idea of how large it is. It should be noted that lithostatic pressure increases linearly towards
the bottom of the plate, unlike the stress σ c,min , which is distributed uniformly across the
plate just as the force F. Both the stress σ c,min and the lithostatic pressure at the base of
of the plate are shown in Figure 9.12 as functions of the plate thickness. The compressive
stress σ c,min is seen to increase as h 1/2 while the lithostatic pressure increases as h.We
can conclude that the deflection of the lithosphere is caused by surface loads, unless it is
compressed by horizontal forces that are much larger than the lithostatic pressure at the
base of the elastic part of the plate.

3.0 800

2.5
600
stress [GPa] 2.0 λ min [km] 400
1.5

1.0
200
0.5

0.0 0
0 10 20 30 40 50 0 10 20 30 40 50
h [km] h [km]
Figure 9.12. (a) The critical stress σ c,min is plotted as a function of the plate thickness. The lithostatic
pressure c gh at the depth h is shown for reference (where c = 2700 kg m −3 is used for the density
of the crust). (b) The wavelength λ min as a function of the plate thickness h.