Page 313 - Physical Principles of Sedimentary Basin Analysis

9.4 Flexure and lateral variations of the load 295

x 0 x 1
−0.2
0.0

0.2
w/w max [−] 0.4

0.6

0.8

1.0
−6 −4 −2 0 2 4 6
x [−]
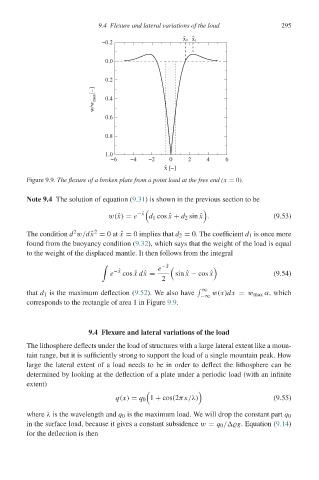
Figure 9.9. The flexure of a broken plate from a point load at the free end (x = 0).

Note 9.4 The solution of equation (9.31) is shown in the previous section to be

x
x
w(ˆ) = e −ˆ d 1 cos ˆx + d 2 sin ˆx . (9.53)
2
2
The condition d w/d ˆx = 0at ˆx = 0 implies that d 2 = 0. The coefficient d 1 is once more
found from the buoyancy condition (9.32), which says that the weight of the load is equal
to the weight of the displaced mantle. It then follows from the integral
e −ˆ
x
x
x
e −ˆ cos ˆxd ˆ = sin ˆ − cos ˆ x (9.54)
x
2
∞
that d 1 is the maximum deflection (9.52). We also have w(x)dx = w max α, which
−∞
corresponds to the rectangle of area 1 in Figure 9.9.
9.4 Flexure and lateral variations of the load
The lithosphere deflects under the load of structures with a large lateral extent like a moun-
tain range, but it is sufficiently strong to support the load of a single mountain peak. How
large the lateral extent of a load needs to be in order to deflect the lithosphere can be
determined by looking at the deflection of a plate under a periodic load (with an infinite
extent)

q(x) = q 0 1 + cos(2πx/λ) (9.55)
where λ is the wavelength and q 0 is the maximum load. We will drop the constant part q 0
in the surface load, because it gives a constant subsidence w = q 0 / g. Equation (9.14)
for the deflection is then