Page 312 - Physical Principles of Sedimentary Basin Analysis

294 Flexure of the lithosphere

5

0
w [km]

−5
point load (3)
Fourier solution
point load (1)
−10
0 200 400 600 800 1000
x [km]
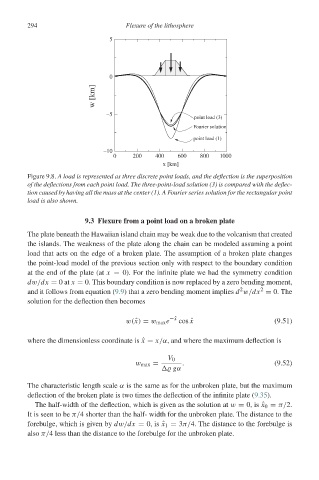
Figure 9.8. A load is represented as three discrete point loads, and the deflection is the superposition
of the deflections from each point load. The three-point-load solution (3) is compared with the deflec-
tion caused by having all the mass at the center (1). A Fourier series solution for the rectangular point
load is also shown.

9.3 Flexure from a point load on a broken plate
The plate beneath the Hawaiian island chain may be weak due to the volcanism that created
the islands. The weakness of the plate along the chain can be modeled assuming a point
load that acts on the edge of a broken plate. The assumption of a broken plate changes
the point-load model of the previous section only with respect to the boundary condition
at the end of the plate (at x = 0). For the infinite plate we had the symmetry condition
dw/dx = 0at x = 0. This boundary condition is now replaced by a zero bending moment,
2
2
and it follows from equation (9.9) that a zero bending moment implies d w/dx = 0. The
solution for the deflection then becomes
x
x
w(ˆ) = w max e −ˆ x cos ˆ (9.51)
x
where the dimensionless coordinate is ˆ = x/α, and where the maximum deflection is

V 0
w max = . (9.52)
gα
The characteristic length scale α is the same as for the unbroken plate, but the maximum
deflection of the broken plate is two times the deflection of the infinite plate (9.35).
x
The half-width of the deflection, which is given as the solution at w = 0, is ˆ 0 = π/2.
It is seen to be π/4 shorter than the half- width for the unbroken plate. The distance to the
forebulge, which is given by dw/dx = 0, is ˆ 1 = 3π/4. The distance to the forebulge is
x
also π/4 less than the distance to the forebulge for the unbroken plate.