Page 315 - Physical Principles of Sedimentary Basin Analysis
P. 315
9.4 Flexure and lateral variations of the load 297
1.0 800
0.8
600
0.6
c [−] λ c [km] 400
0.4
200
0.2
0.0 0
0 1 2 3 4 5 0 10 20 30 40 50
λ/λ [−] h [km]
c
(a) (b)
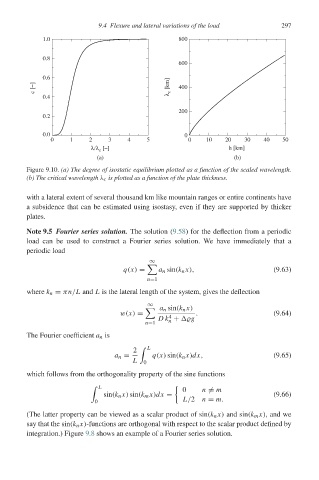
Figure 9.10. (a) The degree of isostatic equilibrium plotted as a function of the scaled wavelength.
(b) The critical wavelength λ c is plotted as a function of the plate thickness.
with a lateral extent of several thousand km like mountain ranges or entire continents have
a subsidence that can be estimated using isostasy, even if they are supported by thicker
plates.
Note 9.5 Fourier series solution. The solution (9.58) for the deflection from a periodic
load can be used to construct a Fourier series solution. We have immediately that a
periodic load
∞
q(x) = a n sin(k n x), (9.63)
n=1
where k n = πn/L and L is the lateral length of the system, gives the deflection
∞
a n sin(k n x)
w(x) = . (9.64)
4
Dk + g
n=1 n
The Fourier coefficient a n is
2 L
a n = q(x) sin(k n x)dx, (9.65)
L 0
which follows from the orthogonality property of the sine functions
L
0 n = m
sin(k n x) sin(k m x)dx = (9.66)
0 L/2 n = m.
(The latter property can be viewed as a scalar product of sin(k n x) and sin(k m x), and we
saythatthesin(k n x)-functions are orthogonal with respect to the scalar product defined by
integration.) Figure 9.8 shows an example of a Fourier series solution.