Page 95 - Physical Principles of Sedimentary Basin Analysis

3.22 Streamlines in 2D 77
Ψ
Ψ B A

B
u
b
u x dy ds
−dx
A
a
u y

(a) (b)
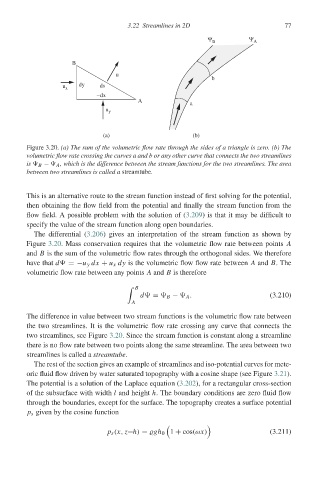
Figure 3.20. (a) The sum of the volumetric flow rate through the sides of a triangle is zero. (b) The
volumetric flow rate crossing the curves a and b or any other curve that connects the two streamlines
is B − A , which is the difference between the stream functions for the two streamlines. The area
between two streamlines is called a streamtube.

This is an alternative route to the stream function instead of first solving for the potential,
then obtaining the flow field from the potential and finally the stream function from the
flow field. A possible problem with the solution of (3.209) is that it may be difficult to
specify the value of the stream function along open boundaries.
The differential (3.206) gives an interpretation of the stream function as shown by
Figure 3.20. Mass conservation requires that the volumetric flow rate between points A
and B is the sum of the volumetric flow rates through the orthogonal sides. We therefore
have that d =−u y dx + u x dy is the volumetric flow flow rate between A and B.The
volumetric flow rate between any points A and B is therefore

B
d = B − A . (3.210)
A
The difference in value between two stream functions is the volumetric flow rate between
the two streamlines. It is the volumetric flow rate crossing any curve that connects the
two streamlines, see Figure 3.20. Since the stream function is constant along a streamline
there is no flow rate between two points along the same streamline. The area between two
streamlines is called a streamtube.
The rest of the section gives an example of streamlines and iso-potential curves for mete-
oric fluid flow driven by water saturated topography with a cosine shape (see Figure 3.21).
The potential is a solution of the Laplace equation (3.202), for a rectangular cross-section
of the subsurface with width l and height h. The boundary conditions are zero fluid flow
through the boundaries, except for the surface. The topography creates a surface potential
p s given by the cosine function

p s (x, z=h) = gh 0 1 + cos(ωx) (3.211)