Page 34 - Physical chemistry eng

1.5 A BRIEF INTRODUCTION TO REAL GASES 11

The ideal gas assumptions that the atoms or molecules of a gas do not interact Real gas Ideal gas
with one another and can be treated as point masses have a limited range of validity,
which can be discussed using the potential energy function typical for a real gas, as
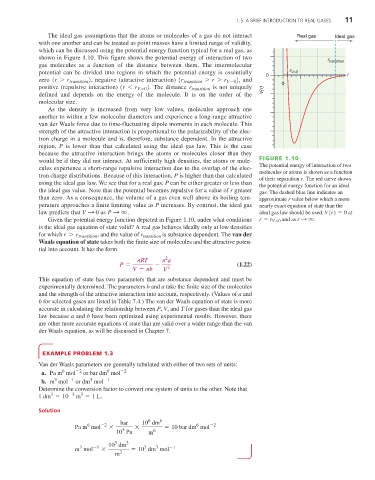
shown in Figure 1.10. This figure shows the potential energy of interaction of two
r transition
gas molecules as a function of the distance between them. The intermolecular
potential can be divided into regions in which the potential energy is essentially r V=0
0 r
zero (r 7 r transition ) , negative (attractive interaction) (r transition 7 r 7 r V=0 ) , and 0
positive (repulsive interaction) (r 6 r V=0 ) . The distance r transition is not uniquely V(r)
defined and depends on the energy of the molecule. It is on the order of the
molecular size.
As the density is increased from very low values, molecules approach one
another to within a few molecular diameters and experience a long-range attractive
van der Waals force due to time-fluctuating dipole moments in each molecule. This
strength of the attractive interaction is proportional to the polarizability of the elec-
tron charge in a molecule and is, therefore, substance dependent. In the attractive
region, P is lower than that calculated using the ideal gas law. This is the case
because the attractive interaction brings the atoms or molecules closer than they
FIGURE 1.10
would be if they did not interact. At sufficiently high densities, the atoms or mole-
The potential energy of interaction of two
cules experience a short-range repulsive interaction due to the overlap of the elec-
molecules or atoms is shown as a function
tron charge distributions. Because of this interaction, P is higher than that calculated
of their separation r. The red curve shows
using the ideal gas law. We see that for a real gas, P can be either greater or less than
the potential energy function for an ideal
the ideal gas value. Note that the potential becomes repulsive for a value of r greater gas. The dashed blue line indicates an
than zero. As a consequence, the volume of a gas even well above its boiling tem- approximate r value below which a more
perature approaches a finite limiting value as P increases. By contrast, the ideal gas nearly exact equation of state than the
law predicts that V : 0 as P : q . ideal gas law should be used. V(r) = 0 at
Given the potential energy function depicted in Figure 1.10, under what conditions r = r V=0 and as r : q .
is the ideal gas equation of state valid? A real gas behaves ideally only at low densities
for which r 7 r transition , and the value of r transition is substance dependent. The van der
Waals equation of state takes both the finite size of molecules and the attractive poten-
tial into account. It has the form
2
nRT n a
P = - (1.22)
V - nb V 2
This equation of state has two parameters that are substance dependent and must be
experimentally determined. The parameters b and a take the finite size of the molecules
and the strength of the attractive interaction into account, respectively. (Values of a and
b for selected gases are listed in Table 7.4.) The van der Waals equation of state is more
accurate in calculating the relationship between P, V, and T for gases than the ideal gas
law because a and b have been optimized using experimental results. However, there
are other more accurate equations of state that are valid over a wider range than the van
der Waals equation, as will be discussed in Chapter 7.

EXAMPLE PROBLEM 1.3
Van der Waals parameters are generally tabulated with either of two sets of units:
6
6
-2
a. Pa m mol or bar dm mol -2
3
3
-1
b. m mol or dm mol -1
Determine the conversion factor to convert one system of units to the other. Note that
3
-3
3
1 dm = 10 m = 1 L .
Solution
6
bar 10 dm 6 6 -2
-2
6
Pa m mol * 5 * = 10 bar dm mol
10 Pa m 6
3
10 dm 3 3 3 -1
3
-1
m mol * 3 = 10 dm mol
m