Page 31 - Physical chemistry eng

8 CHAPTER 1 Fundamental Concepts of Thermodynamics

where T is the absolute temperature as defined by Equation (1.16), allowing a to be
a
determined. The constant is found to be directly proportional to the mass of gas used.
4
It is useful to separate this dependence by writing a = nR , where n is the number of
moles of the gas, and R is a constant that is independent of the size of the system. The
result is the ideal gas equation of state (1.18)
3
Pressure/10 6 Pa 2 as derived in Equation (1.11). The equation of state given in Equation (1.18) is familiar
PV = Nk T = nRT
B
as the ideal gas law. Because the four variables P, V, T, and n are related through the

700 K equation of state, any three of these variables is sufficient to completely describe the
ideal gas.
1 Of these four variables, P and T are independent of the amount of gas, whereas V
and n are proportional to the amount of gas. A variable that is independent of the size of
200 K the system (for example, P and T) is referred to as an intensive variable, and one that
is proportional to the size of the system (for example, V) is referred to as an extensive
variable. Equation (1.18) can be written in terms of intensive variables exclusively:
0.2 0.4 0.6 0.8 1.0 1.2 1.4
Volume/10 2 m 3 P = r RT (1.13)
m
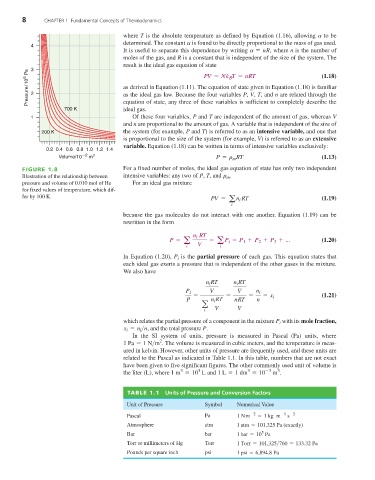
FIGURE 1.8 For a fixed number of moles, the ideal gas equation of state has only two independent
Illustration of the relationship between intensive variables: any two of P, T, and r m .
pressure and volume of 0.010 mol of He For an ideal gas mixture
for fixed values of temperature, which dif-
fer by 100 K. PV = a i (1.19)
n RT
i
because the gas molecules do not interact with one another. Equation (1.19) can be
rewritten in the form

n RT
i
P = = P = P + P + P + ... (1.20)
2
3
i
1
a V a
i i
In Equation (1.20), P is the partial pressure of each gas. This equation states that
i
each ideal gas exerts a pressure that is independent of the other gases in the mixture.
We also have
n RT n RT
i
i
P i = V = V = n i = x (1.21)
P n RT nRT n i
i

a V V
i
which relates the partial pressure of a component in the mixture P with its mole fraction,
i
x = n >n , and the total pressure P.
i
i
In the SI system of units, pressure is measured in Pascal (Pa) units, where
1 Pa = 1 N>m 2 . The volume is measured in cubic meters, and the temperature is meas-
ured in kelvin. However, other units of pressure are frequently used, and these units are
related to the Pascal as indicated in Table 1.1. In this table, numbers that are not exact
have been given to five significant figures. The other commonly used unit of volume is
3
3
3
-3
the liter (L), where 1 m = 10 L and 1 L = 1 dm = 10 m 3 .
TABLE 1.1 Units of Pressure and Conversion Factors
Unit of Pressure Symbol Numerical Value
-1 -2
Pascal Pa 1 Nm -2 = 1 kg m s
Atmosphere atm 1 atm = 101,325 Pa (exactly)
5
Bar bar 1 bar = 10 Pa
Torr or millimeters of Hg Torr 1 Torr = 101,325>760 = 133.32 Pa
Pounds per square inch psi 1 psi = 6,894.8 Pa