Page 244 - Physical Chemistry

lev38627_ch07.qxd 3/14/08 12:51 PM Page 225

225
Section 7.5
3
1
J 82.06 cm atm mol K 1 Higher-Order Phase Transitions
P 1 bar 1506 3 1 1 14900 atm
2
cm 8.314 J mol K
P 14900 atm 15100 bar
2
Thus, above 15.1 kbar, diamond is predicted to be the more-stable phase. When
the pressure dependence of V m is allowed for, the calculated transition pressure
becomes 16.3 kbar. In actuality, just as diamond will persist indefinitely at room
T and P even though it is metastable with respect to graphite, graphite will per-
sist indefinitely at room temperature and pressures above 16.3 kbar. Conversion
of graphite to diamond is done in the laboratory by increasing both P and T in
the presence of a catalyst. There is a large activation-energy barrier (Sec. 16.8)
involved in converting the “infinite” two-dimensional covalent-bond structure
of graphite to the “infinite” three-dimensional covalent structure of diamond
(Fig. 23.19). Thermodynamics cannot tell us about rates of processes.

Exercise
The solid–liquid–gas triple point of carbon is at 5000 K and 100 bar and the
5
diamond–graphite–liquid triple point is at 4900 K and 10 bar. The graphite melt-
ing line shows a maximum temperature and the diamond melting line has a pos-
itive dP/dT at lower temperatures and shows a maximum temperature at higher T.
4
The critical point is at roughly 6800 K and 2 10 bar. Sketch the phase diagram
of carbon using a logarithmic scale for pressure. [Answer: See F. P. Bundy et al.,
Carbon, 34, 141 (1996); X. Wang, Phys. Rev. Lett., 95, 185701 (2005).]

One-component solid–solid transitions between different structural forms are
3
common. One-component liquid–liquid phase transitions are rare but occur in He and
4 He (Sec. 7.5) and there is some evidence for such phase transitions in liquid sulfur,
selenium, and iodine [P. F. McMillan et al., J. Phys.: Condens. Matter, 19, 415101
(2007)].

7.5 HIGHER-ORDER PHASE TRANSITIONS
For the equilibrium phase transitions at constant T and P discussed in Secs. 7.2 to 7.4,
the transition is accompanied by a transfer of heat q 0 between system and sur-
P
roundings; also, the system generally undergoes a volume change. Such transitions
with H 0 are called first order or discontinuous.
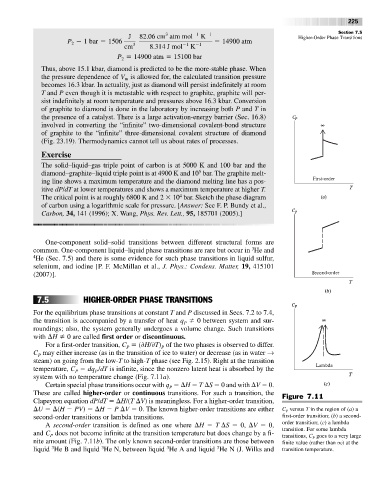
For a first-order transition, C ( H/ T) of the two phases is observed to differ.
P
P
C may either increase (as in the transition of ice to water) or decrease (as in water →
P
steam) on going from the low-T to high-T phase (see Fig. 2.15). Right at the transition
temperature, C dq /dT is infinite, since the nonzero latent heat is absorbed by the
P P
system with no temperature change (Fig. 7.11a).
Certain special phase transitions occur with q H T S 0 and with V 0.
P
These are called higher-order or continuous transitions. For such a transition, the Figure 7.11
Clapeyron equation dP/dT H/(T V) is meaningless. For a higher-order transition,
U (H PV) H P V 0. The known higher-order transitions are either C versus T in the region of (a) a
P
second-order transitions or lambda transitions. first-order transition; (b) a second-
A second-order transition is defined as one where H T S 0, V 0, order transition; (c) a lambda
transition. For some lambda
and C does not become infinite at the transition temperature but does change by a fi-
P transitions, C goes to a very large
P
nite amount (Fig. 7.11b). The only known second-order transitions are those between finite value (rather than q) at the
3
3
3
3
liquid He B and liquid He N, between liquid He A and liquid He N (J. Wilks and transition temperature.