Page 293 - Physical Chemistry

lev38627_ch09.qxd 3/14/08 1:31 PM Page 274

274
Chapter 9
Solutions

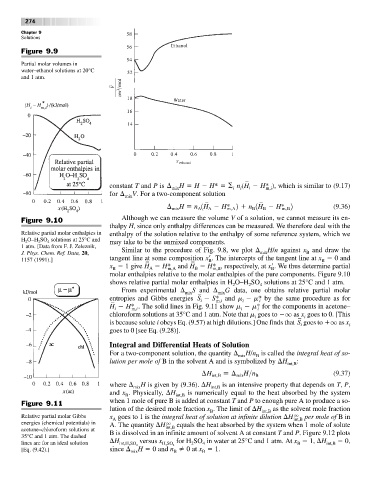
Figure 9.9
Partial molar volumes in
water–ethanol solutions at 20°C
and 1 atm.

constant T and P is ¢ mix H H H* i n (H i H* ), which is similar to (9.17)
m,i
i
for ¢ mix V. For a two-component solution

¢ mix H n 1H H* 2 n 1H H* 2 (9.36)
B
B
A
m,B
A
m,A
Figure 9.10 Although we can measure the volume V of a solution, we cannot measure its en-
thalpy H, since only enthalpy differences can be measured. We therefore deal with the
Relative partial molar enthalpies in enthalpy of the solution relative to the enthalpy of some reference system, which we
H O–H SO solutions at 25°C and may take to be the unmixed components.
2
2
4
1 atm. [Data from F. J. Zeleznik, Similar to the procedure of Fig. 9.8, we plot H/n against x and draw the
J. Phys. Chem. Ref. Data, 20, mix B
1157 (1991).] tangent line at some composition x . The intercepts of the tangent line at x 0 and
B
B

x 1 give H A H* and H B H* , respectively, at x . We thus determine partial
m,B
B
m,A
B
molar enthalpies relative to the molar enthalpies of the pure components. Figure 9.10
shows relative partial molar enthalpies in H O–H SO solutions at 25°C and 1 atm.
4
2
2
From experimental mix S and mix G data, one obtains relative partial molar

entropies and Gibbs energies S i S* and m i m * by the same procedure as for
i
m,i

H i H* . The solid lines in Fig. 9.11 show m i m * for the components in acetone–
i
m,i
chloroform solutions at 35°C and 1 atm. Note that m goes to q as x goes to 0. [This
i
i

is because solute i obeys Eq. (9.57) at high dilutions.] One finds that S i goes to q as x i
goes to 0 [see Eq. (9.28)].
Integral and Differential Heats of Solution
For a two-component solution, the quantity mix H/n is called the integral heat of so-
B
lution per mole of B in the solvent A and is symbolized by H int,B :
¢H int,B ¢ mix H>n B (9.37)
where mix H is given by (9.36). H int,B is an intensive property that depends on T, P,
and x . Physically, H int,B is numerically equal to the heat absorbed by the system
B
Figure 9.11 when 1 mole of pure B is added at constant T and P to enough pure A to produce a so-
lution of the desired mole fraction x . The limit of H int,B as the solvent mole fraction
B
Relative partial molar Gibbs x goes to 1 is the integral heat of solution at infinite dilution H int,B per mole of B in
q
A
energies (chemical potentials) in A. The quantity H q equals the heat absorbed by the system when 1 mole of solute
int,B
acetone–chloroform solutions at B is dissolved in an infinite amount of solvent A at constant T and P. Figure 9.12 plots
35°C and 1 atm. The dashed
lines are for an ideal solution H int,H 2 SO 4 versus x H 2 SO 4 for H SO in water at 25°C and 1 atm. At x 1, H int,B 0,
B
4
2
[Eq. (9.42).] since mix H 0 and n 0 at x 1.
B
B