Page 101 - Plastics Engineering

84 Mechanical Behaviour of Plastics

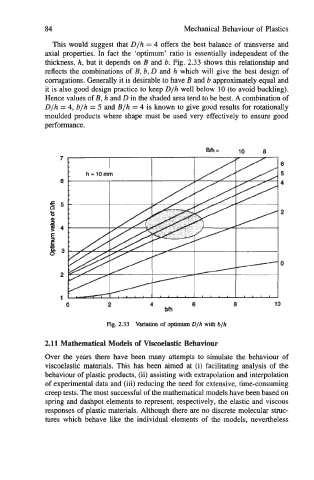
This would suggest that D/h = 4 offers the best balance of transverse and
axial properties. In fact the ‘optimum’ ratio is essentially independent of the
thickness, h, but it depends on B and b. Fig. 2.33 shows this relationship and
reflects the combinations of B, b, D and h which will give the best design of
cormgations. Generally it is desirable to have B and b approximately equal and
it is also good design practice to keep D/h well below 10 (to avoid buckling).
Hence values of B, h and D in the shaded area tend to be best. A combination of
D/h = 4, b/h = 5 and B/h = 4 is known to give good results for rotationally
moulded products where shape must be used very effectively to ensure good
performance.

B/h= 10 8
7

6

I

8 3

2

1
0 2 4 6 8 10
wh

Fig. 2.33 Variation of optimum Dlh with blh

2.11 Mathematical Models of Viioelastic Behaviour
Over the years there have been many attempts to simulate the behaviour of
viscoelastic materials. This has been aimed at (i) facilitating analysis of the
behaviour of plastic products, (ii) assisting with extrapolation and interpolation
of experimental data and (iii) reducing the need for extensive, time-consuming
creep tests. The most successful of the mathematical models have been based on
spring and dashpot elements to represent, respectively, the elastic and viscous
responses of plastic materials. Although there are no discrete molecular struc-
tures which behave like the individual elements of the models, nevertheless