Page 182 - Plastics Engineering

Mechanical Behaviour of Plastics 165

2.46 For the type of Standard Linear Solid described in Q 2.33, derive equations for the storage
modulus, the loss modulus and tan S when the material is subjected to a sinusoidally varying stress.
Confirm that for 9 = 1 GNs/m2, el = 2 GN/m2 and 42 = 0.1 GN/m2, your equations predict the
classical variation of E,, E2 and tan6 for values of w in the range 0.01 to 100 s-'.
2.47 Creep rupture tests on a particular grade of uPVC at 20°C gave the following results for
applied stress, u, and time to failure, t.
Stress (MN/m2) 60 55 52 48 45 43
time(s) 800 7 x lo3 3.25 x lo4 2.15 x Id 8.9 x IO6 2.4 x lo6
Confirm that this data obeys a law of the form

and determine the values of the constants A and B.
2.48 For the material in the previous question, use the Zhurkov-Beuche equation to calculate
the time to failure under a steady stress of 44 MN/m2 if the material temperature is 40°C. The
activation energy, UO, may be taken as 150 kJ/mol.
2.49 A 200 mm diameter plastic pipe is to be subjected to an internal pressure of 0.5 MN/m2
for 3 years. If the creep rupture behaviour of the material is as shown in Fig. 3.10, calculate a
suitable wall thickness for the pipe. You should use a safety factor of 1.5.
2.50 Fracture Mechanics tests on a grade of ABS indicate that its K value is 2 MN m-3/2 and
that under static loading its growth rate is described by the equation.

daldt = 3 x 10-"K3.2
where K has units MN mP3l2. If, in service, the material is subjected to a steady stress of
20 MN/mz estimate the maximum defect size which could be tolerated in the material if it is to
last for at least 1 year.
2.51 Use the data in Table 2.2 to compare crack tip plastic zone sizes in acrylic, ABS and
polypropylene.
2.52 In a tensile test on an un-notched sample of acrylic the fracture stress is recorded as
57 MN/m2. Estimate the likely size of the intrinsic defects in the material.
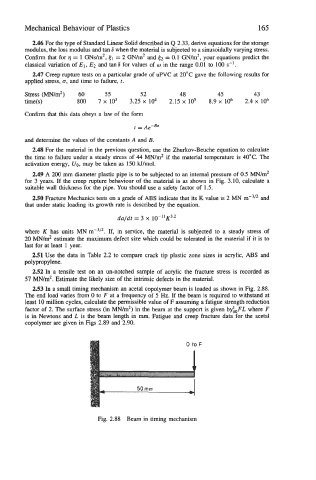
2.53 In a small timing mechanism an acetal copolymer beam is loaded as shown in Fig. 2.88.
The end load varies from 0 to F at a frequency of 5 Hz. If the beam is required to withstand at
least 10 million cycles, calculate the permissible value of F assuming a fatigue strength reduction
factor of 2. The surface stress (in MN/m2) in the beam at the support is given by@. where F
is in Newtons and L is the beam length in mm. Fatigue and creep fracture data for the acetal
copolymer are given in Figs 2.89 and 2.90.

Fig. 2.88 Beam in timing mechanism