Page 206 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

180 Chapter Seven

1
0.95 ......
0.9
0.85 . . .. .. . . '. • • I • •
~ 0.8 .. . . . .
e
Ill 0.75 ..
~
~ 0.7
0.65

0.6
0.55
0.50
0.5 1 1.5 2 2.5 3 3.5 4
Axial distance z

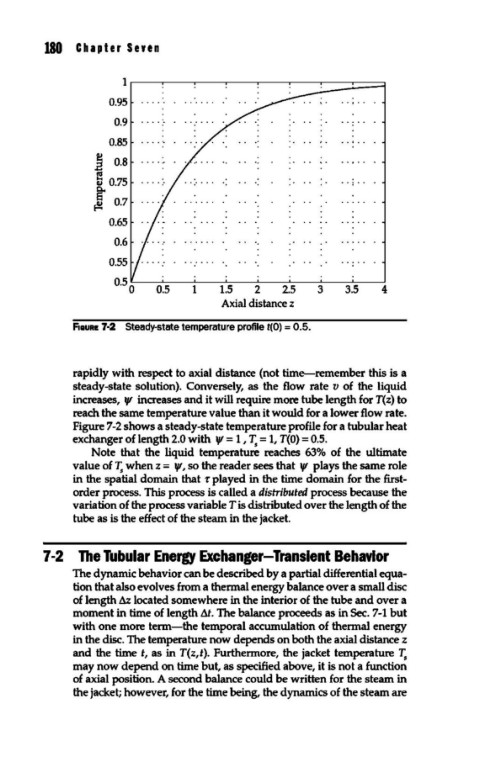
fiGURE 7·2 Steady-state temperature profile t(O) = 0.5.

rapidly with respect to axial distance (not time-remember this is a
steady-state solution). Conversely, as the flow rate v of the liquid
increases, yt increases and it will require more tube length for T(z) to
reach the same temperature value than it would for a lower flow rate.
Figure 7-2 shows a steady-state temperature profile for a tubular heat
exchanger of length 2.0 with yt = 1 , ~ = 1, T(O) = 0.5.
Note that the liquid temperature reaches 63% of the ultimate
value of~ when z = yt, so the reader sees that yt plays the same role
in the spatial domain that 'f played in the time domain for the first-
order process. This process is called a distributed process because the
variation of the process variable Tis distributed over the length of the
tube as is the effect of the steam in the jacket.

7-2 The Tubular Energy Exchanger-Transient Behavior
The dynamic behavior can be described by a partial differential equa-
tion that also evolves from a thermal energy balance over a small disc
of length Az located somewhere in the interior of the tube and over a
moment in time of length At. The balance proceeds as in Sec. 7-1 but
with one more term-the temporal accumulation of thermal energy
in the disc. The temperature now depends on both the axial distance z
and the time t, as in T(z,t). Furthermore, the jacket temperature ~
may now depend on time but, as specified above, it is not a function
of axial position. A second balance could be written for the steam in
the jacket; however, for the time being, the dynamics of the steam are