Page 78 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

Basic Concepts in Process Analysis 53

2
(1 + gk) > 4-rgi
so, (3-27)
I< (1+ gk)2
4-rg

(Note how this integral gain I is less than that for the critically damped
case.)
Since there are two roots, the solution will have the form

(3-28)
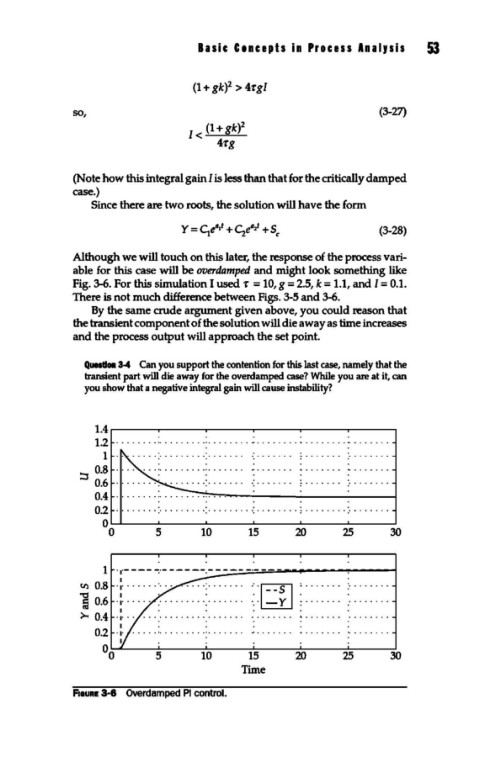
Although we will touch on this later, the response of the process vari-
able for this case will be overdamped and might look something like
Fig. 3-6. For this simulation I used -r = 10, g = 2.5, k = 1.1, and I= 0.1.
There is not much difference between Figs. 3-5 and 3-6.
By the same crude argument given above, you could reason that
the transient component of the solution will die away as time increases
and the process output will approach the set point.

Question 3-4 Can you support the contention for this last case, namely that the
transient part will die away for the overdamped case? While you are at it, can
you show that a negative integral gain will cause instability?

1.4 .-------r------.------,r----...------.------,
1.2 .......................... 0 ••••••••• 0 ................. .
1
::s 0.8
0.6
0.4
•
•
0.2 • • • • • • • • • • • •••••••••••••••• 0 • •••••••• 0 0 : ••••••• 0 • : •••••••
0~----~----~------~----~------L-----~
0 5 10 15 20 25 30

1 0 .. ---- -:·- --- --. -:..:-:.=..-=-·..:.-.::-;:·-~-:.::-=-=-......... --~~--1
U') 0.8 ·:·F-51
1 0.6 ·.·L=r_j
>- 0.4
0.2

5 10 15 20 25 30
Time
F1auRE 3-6 OVerdamped PI control.