Page 81 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

56 Chapter Three

1.4 r------r-----.---.-------,-r=====,-,
- P-only
-- PI under
1.2
.. ~ -.- - · · · PI over
. ,' ·-·Picrit
... :.,''. ~.·~·~··--.:~:.~~:~~~:=:::-:--:.;.!:.:::-.:.:-.:.~•.::::.~-;:.~-:-~·
1
:1 ~ •••
"E I ,· •• ••
," •••
to.s . /':/."····· .... _· ·----------------1
I•
0
~ ,' ,:··
,. 1::·· ..
~ 0.6
e , ..
I,::
Q..,
·~· .
0.4 . J('
·~·
J:'
t
0.2
~
5 10 15 20 25 30
Time
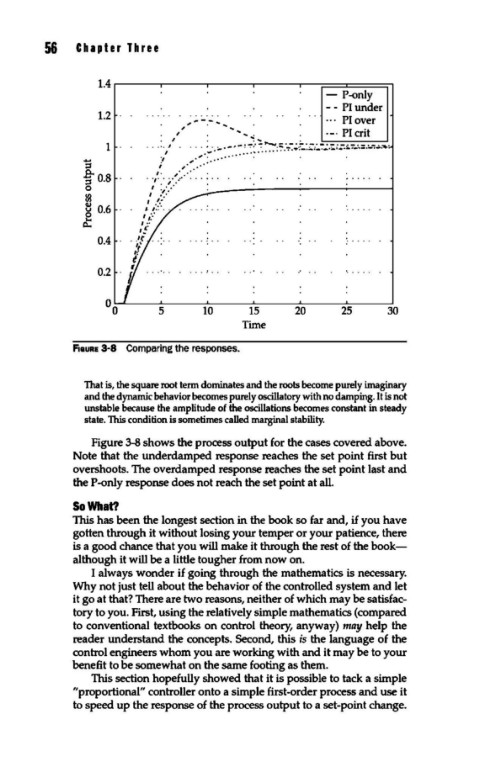
F1auRE 3-8 Comparing the responses.
That is, the square root term dominates and the roots become purely imaginary
and the dynamic behavior becomes purely oscillatory with no damping. It is not
unstable because the amplitude of the oscillations becomes constant in steady
state. This condition is sometimes called marginal stability.
Figure 3-8 shows the process output for the cases covered above.
Note that the underdamped response reaches the set point first but
overshoots. The overdamped response reaches the set point last and
the P-only response does not reach the set point at all.
So What?
This has been the longest section in the book so far and, if you have
gotten through it without losing your temper or your patience, there
is a good chance that you will make it through the rest of the book-
although it will be a little tougher from now on.
I always wonder if going through the mathematics is necessary.
Why not just tell about the behavior of the controlled system and let
it go at that? There are two reasons, neither of which may be satisfac-
tory to you. First, using the relatively simple mathematics (compared
to conventional textbooks on control theory, anyway) may help the
reader understand the concepts. Second, this is the language of the
control engineers whom you are working with and it may be to your
benefit to be somewhat on the same footing as them.
This section hopefully showed that it is possible to tack a simple
"proportional" controller onto a simple first-order process and use it
to speed up the response of the process output to a set-point change.