Page 77 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

52 Chapter Three

1.4 .-----~-----.-------.-----r--------r------.
1.2
1
::s 0.8
0.6
0.4
0.2
00 5 10 15 20 25 30

1
U') 0.8
"'tS : :F-51: :
fa 0.6 ::::: :~:::::::: :~ -~-: ~:::::::: ~::::
>- 0.4
0 • • 0
0.2 .......................................
0 0 0 0
00 5 10 15 20 25 30
Time

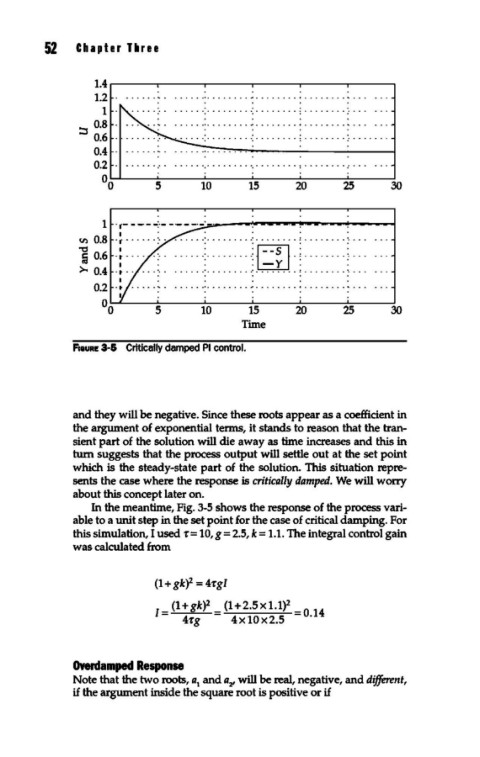
F1auRE 3-5 Critically damped PI control.

and they will be negative. Since these roots appear as a coefficient in
the argument of exponential terms, it stands to reason that the tran-
sient part of the solution will die away as time increases and this in
tum suggests that the process output will settle out at the set point
which is the steady-state part of the solution. This situation repre-
sents the case where the response is critically damped. We will worry
about this concept later on.
In the meantime, Fig. 3-5 shows the response of the process vari-
able to a unit step in the set point for the case of critical damping. For
this simulation, I used -r= 10, g = 2.5, k = 1.1. The integral control gain
was calculated from

2
(1 + gk) = 4-rgl
(1 + 2.5 X 1.1) 2
4x10x2.5 °· 14

Overdamped Response
Note that the two roots, a and a2' will be real, negative, and different,
1
if the argument inside the square root is positive or if