Page 98 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

Basic Concepts in Process Analysis 73

1000
800

600
400

200
0
5

Imaginary part of s
-5 Real part of s
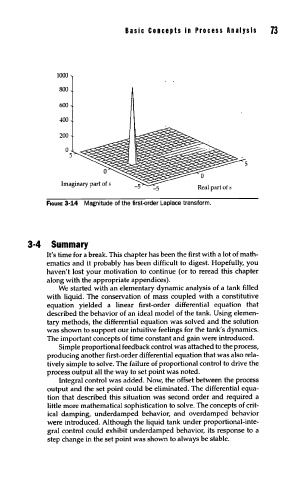
fiGURE 3-14 Magnitude of the first-order Laplace transform.

3-4 Summary
It's time for a break. This chapter has been the first with a lot of math-
ematics and it probably has been difficult to digest. Hopefully, you
haven't lost your motivation to continue (or to reread this chapter
along with the appropriate appendices).
We started with an elementary dynamic analysis of a tank filled
with liquid. The conservation of mass coupled with a constitutive
equation yielded a linear first-order differential equation that
described the behavior of an ideal model of the tank. Using elemen-
tary methods, the differential equation was solved and the solution
was shown to support our intuitive feelings for the tank's dynamics.
The important concepts of time constant and gain were introduced.
Simple proportional feedback control was attached to the process,
producing another first-order differential equation that was also rela-
tively simple to solve. The failure of proportional control to drive the
process output all the way to set point was noted.
Integral control was added. Now, the offset between the process
output and the set point could be eliminated. The differential equa-
tion that described this situation was second order and required a
little more mathematical sophistication to solve. The concepts of crit-
ical damping, underdamped behavior, and overdamped behavior
were introduced. Although the liquid tank under proportional-inte-
gral control could exhibit underdamped behavior, its response to a
step change in the set point was shown to always be stable.