Page 267 - Practical Design Ships and Floating Structures

242

requires the definition of a limit state function G(x) through a user-defined subroutine, ULIMIT. The
ULTSTR deterministic solver is integrated in ULIMIT using a system call to execute the ULTSTR
response analysis module. While PULSTR provides fourteen (14) analytical statistical modes in its
probability distribution library, an arbitrary user-defined probability distribution can be specified with
the use of user-defined subroutine, UCPDF.

EXAMPLE APPLICATIONS OF PULSTR
In order to perform reliability assessment of a hull girder under random longitudinal bending, a limit
state function G(x) has to be defined with the user-defined subroutine, ULIMIT. For a given vector of
random variables x(z1, 22, z3, ..., z,, MSW, Mw~) characterizing randomness in hull geometry, panel
thickness, stiffener parameters, hard corner parameters, material parameters, and loading parameters
(Msw, MwD), the limit state function can be expressed as
(3x1 = M,,,, (2, z2r”‘r 2,) -Ma,, (MSW M,,) (3)
3
2
where Mul, is the ultimate resisting moment of a hull section computed by ULTSTR, and Mapp is the
resultant applied bending moment induced by the stillwater bending moment (Msw) and the combined
wave-induced and dynamic bending moment (MwD). Since the probability of failure of a hull girder is
in the range of IO” to the computational effort associated with a direct application of Monte Carlo
simulation (MCS) will be prohibitively large, thus precluding its use for reliability assessment of
surface ships. While the first order reliability method (FORM) provides an alternative way for
evaluating the small probability of failure, the direct application of Eq. (3) in PULSTR’s FORM
solution module will result in a divergent solution because of 1) the oscillation of G(x) near the design
point (x”); and 2) nonlinear dependence of the hull capacity Mutt on hull parameters zi (i=l, 2, ..., n).
To circumvent this difficulty, a hybrid approach is developed where a relatively small number of
MCSs is performed to generate the statistical distribution of Muif and the PULSTR’s FORM solution
module is applied next by replacing A4,,/f(z1, 22, ..., zn) in Eq. (3) with one independent random variable

= 7 00E-10 1
-
.-
0
CI MaPP
2 6.00E-10
-
3
LL
> 5.00E-10
.-
cn
5 4.00E-10
n
-
.- 3 3.00E-10
.-
Q
2 2.00E-10
0
L
5 1.00E-10
LL
O ~-
n O.OOE+OO
O.OE+OO 5.OE+09 I.OE+IO 1.5E+10 2.OE+10 2.5E+10
M - Moment (Ib in)
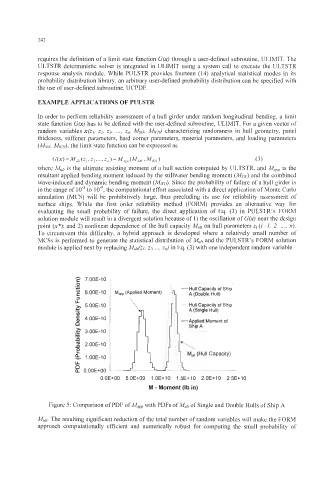
Figure 5: Comparison of PDF of Mapp with PDFs of Mu/, of Single and Double Hulls of Ship A
Mu/,. The resulting significant reduction of the total number of random variables will make the FORM
approach computationally efficient and numerically robust for computing the small probability of