Page 471 - Practical Design Ships and Floating Structures

446

The desingularization method was first developed by von Karman [ 131 in which an axial source
distribution was used to determine the flow about an axisymmetric body. A non-singular formulation
of the boundary integral equation method was proposed by Kupradze [7]. The exterior Dirichlet
problem was solved by using an auxiliary surface located outside the computational domain. Webster
[ 141 investigated the numerical properties of the desingularization technique .for the external potential
flow around an arbitrary, three-dimensional smooth body. He concluded that the use of this
desingularization technique greatly improved the accuracy of the solution.

Cao, Schultz & Beck [2, 3, 41 solved nonlinear problems for waves generated by a free surface
pressure disturbance or a submerged body by combining the time-stepping scheme and the
desingularized boundary integral equation method. Cao, Lee & Beck [l] extended the method to study
nonlinear water wave problems with floating bodies, Scorpio et a1 191 used a multipole accelerated
desingularized method to compute nonlinear water waves. Lee & Cheng [lo, 111 used the
desingularized method to solve hlly nonlinear wave calculations for arbitrary float bodies.

2 FULLY NONLINEAR PROBLEM FORMULATION
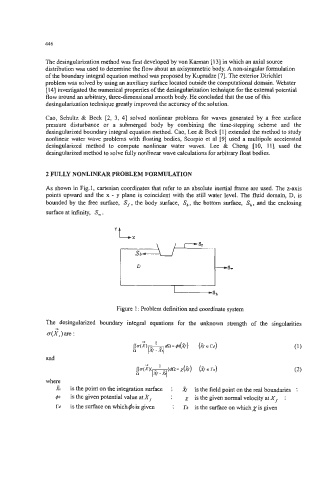
As shown in Fig.1, Cartesian coordinates that refer to an absolute inertial frame are used. The z-axis
points upward and the x - y plane is coincident with the still water level. The fluid domain, D, is
bounded by the fkee surface, Sf, the body surface, S,, the bottom surface, S,, and the enclosing
surface at infinity, S, .

Figure 1 : Problem definition and coordinate system

The desingularized boundary integral equations for the unknown strength of the singularities
-b
a(X*)are :

and

where
L is the point on the integration surface : 3 is the field point on the real boundaries ;
40 is the given potential value at X, * x is the given normal velocity at X, ;
rd is the surface on which (60 is given : li, is the surface on which x is given