Page 246 - Principles and Applications of NanoMEMS Physics

236 Appendix B

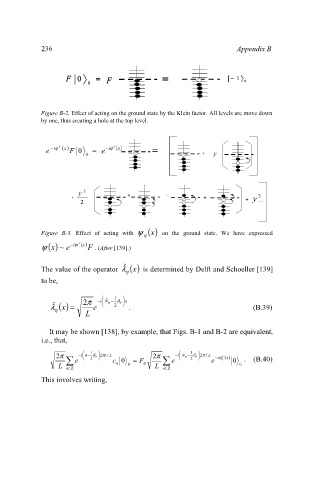
F F 0 0 = = F F = = − − 1 1
0 0 0 0

Figure B-2. Effect of acting on the ground state by the Klein factor. All levels are move down
by one, thus creating a hole at the top level.

()
− iϕ () i − ϕ i − ϕ + + () ()x x = =
+ +
− iϕ
x x
= e e
e e F F 0 0 =
0 0 + + y y
y y 2 2 + + - -
+ + + + 3 3
+ y …
2 2 + y …

Figure B-3. Effect of acting with ψ η () x on the ground state. We have expressed

ψ () x ~ e i − ϕ + () F . (After [139].)
x

The value of the operator () xλ is determined by Delft and Schoeller [139]
ˆ
η
to be,
1
ˆ
η
λ () x = 2 π e − i¨ § © N − δ b · ¹ x ¸ . (B.39)
ˆ
2
η
L
It may be shown [138], by example, that Figs. B-1 and B-2 are equivalent,
i.e., that,
1
2π ¦ e −i § ¨ −n 1 2 b δ · ¸2 x π / L c 0 = F 2π ¦ e −i § ¨ N η − δ b · ¸2π / L e −i η + () x 0 . (B.40)
ϕ
¹
2
©
¹
©
L n ∈Z n 0 η L n ∈Z 0
This involves writing,