Page 95 - Process Equipment and Plant Design Principles and Practices by Subhabrata Ray Gargi Das

92 Chapter 4 Shell and tube heat exchanger

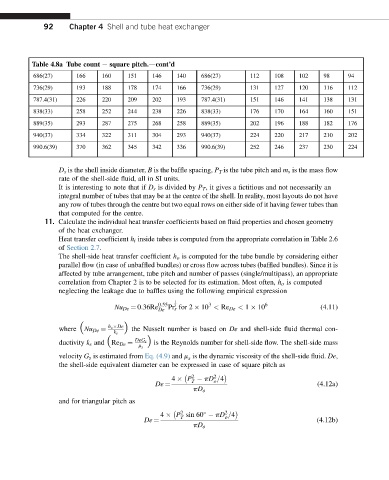
Table 4.8a Tube count e square pitch.dcont’d
686(27) 166 160 151 146 140 686(27) 112 108 102 98 94
736(29) 193 188 178 174 166 736(29) 131 127 120 116 112
787.4(31) 226 220 209 202 193 787.4(31) 151 146 141 138 131
838(33) 258 252 244 238 226 838(33) 176 170 164 160 151
889(35) 293 287 275 268 258 889(35) 202 196 188 182 176
940(37) 334 322 311 304 293 940(37) 224 220 217 210 202
990.6(39) 370 362 345 342 336 990.6(39) 252 246 237 230 224

D s is the shell inside diameter, B is the baffle spacing, P T is the tube pitch and m s is the mass flow
rate of the shell-side fluid, all in SI units.
It is interesting to note that if D s is divided by P T , it gives a fictitious and not necessarily an
integral number of tubes that may be at the centre of the shell. In reality, most layouts do not have
any row of tubes through the centre but two equal rows on either side of it having fewer tubes than
that computed for the centre.
11. Calculate the individual heat transfer coefficients based on fluid properties and chosen geometry
of the heat exchanger.
Heat transfer coefficient h i inside tubes is computed from the appropriate correlation in Table 2.6
of Section 2.7.
The shell-side heat transfer coefficient h o is computed for the tube bundle by considering either
parallel flow (in case of unbaffled bundles) or cross flow across tubes (baffled bundles). Since it is
affected by tube arrangement, tube pitch and number of passes (single/multipass), an appropriate
correlation from Chapter 2 is to be selected for its estimation. Most often, h o is computed
neglecting the leakage due to baffles using the following empirical expression
1
0:55 3 6
Nu De ¼ 0:36Re Pr s for 2 10 < Re De < 1 10 (4.11)
3
De
h o De
Þ the Nusselt number is based on De and shell-side fluid thermal con-
where ðNu De ¼
k s
DeG s
ductivity k s and ðRe De ¼ Þ is the Reynolds number for shell-side flow. The shell-side mass
m s
velocity G s is estimated from Eq. (4.9) and m is the dynamic viscosity of the shell-side fluid. De,
s
the shell-side equivalent diameter can be expressed in case of square pitch as
2 2
4 P pD =4
o
T
(4.12a)
De ¼
pD o
and for triangular pitch as
2 2
4 P sin 60 pD =4

T o
(4.12b)
De ¼
pD o