Page 170 - Process Modelling and Simulation With Finite Element Methods

Extended Multiphysics 157

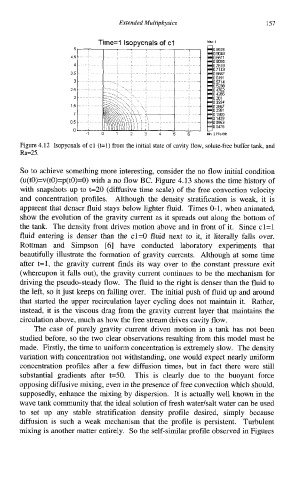
Time=l lsopycnals of cl Max 1

35

0 0476
z
1 0 1 2 3 4 5 6 MN~ rre DO.
Figure 4.12 Isopycnals of cl (t=l) from the initial state of cavity flow, solute-free buffer tank, and
Ra=25.

So to achieve something more interesting, consider the no flow initial condition
(u(tO)=v(tO)=p(tO)=O) with a no flow BC. Figure 4.13 shows the time history of
with snapshots up to t=20 (diffusive time scale) of the free convection velocity
and concentration profiles. Although the density stratification is weak, it is
apparent that denser fluid stays below lighter fluid. Times 0-1, when animated,
show the evolution of the gravity current as it spreads out along the bottom of
the tank. The density front drives motion above and in front of it. Since cl=l
fluid entering is denser than the cl=O fluid next to it, it literally falls over.
Rottman and Simpson [6] have conducted laboratory experiments that
beautifully illustrate the formation of gravity currents. Although at some time
after t=l, the gravity current finds its way over to the constant pressure exit
(whereupon it falls out), the gravity current continues to be the mechanism for
driving the pseudo-steady flow. The fluid to the right is denser than the fluid to
the left, so it just keeps on falling over. The initial push of fluid up and around
that started the upper recirculation layer cycling does not maintain it. Rather,
instead, it is the viscous drag from the gravity current layer that maintains the
circulation above, much as how the free stream drives cavity flow.
The case of purely gravity current driven motion in a tank has not been
studied before, so the two clear observations resulting from this model must be
made. Firstly, the time to uniform concentration is extremely slow. The density
variation with concentration not withstanding, one would expect nearly uniform
concentration profiles after a few diffusion times, but in fact there were still
substantial gradients after t=50. This is clearly due to the buoyant force
opposing diffusive mixing, even in the presence of free convection whch should,
supposedly, enhance the mixing by dispersion. It is actually well known in the
wave tank community that the ideal solution of fresh waterhalt water can be used
to set up any stable stratification density profile desired, simply because
diffusion is such a weak mechanism that the profile is persistent. Turbulent
mixing is another matter entirely. So the self-similar profile observed in Figures