Page 210 - Process Modelling and Simulation With Finite Element Methods

Simulation and Nonlinear Dynamics 197

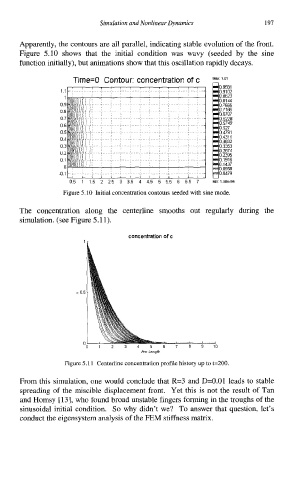
Apparently, the contours are all parallel, indicating stable evolution of the front.
Figure 5.10 shows that the initial condition was wavy (seeded by the sine
function initially), but animations show that this oscillation rapidly decays.
Time=O Contour: concentration of c Max 1 01
0 9581
11 0 9102
1 0 8623
0 8144
09 0 7665
08 0 7186
0 6707
07 0 6228
06 0 5749
0 527
05 0 4791
04 04311
0 3832
03 0 3353
02 0 2874
0 2395
01 0 1916
0 0 1437
0 0958
01 0 0479
05 1 15 2 25 3 35 4 45 5 55 6 65 7 MI" 198e-04'
Figure 5.10 Initial concentration contours seeded with sine mode.
The concentration along the centerline smooths out regularly during the
simulation. (see Figure 5.1 1).
concentration of c

Arc Length
Figure 5.1 1 Centerline concentration profile history up to t=200
From this simulation, one would conclude that R=3 and D=0.01 leads to stable
spreading of the miscible displacement front. Yet this is not the result of Tan
and Homsy [13], who found broad unstable fingers forming in the troughs of the
sinusoidal initial condition. So why didn't we? To answer that question, let's
conduct the eigensystem analysis of the FEM stiffness matrix.