Page 116 - Reliability and Maintainability of In service Pipelines

Time-Dependent Reliability Analysis 105

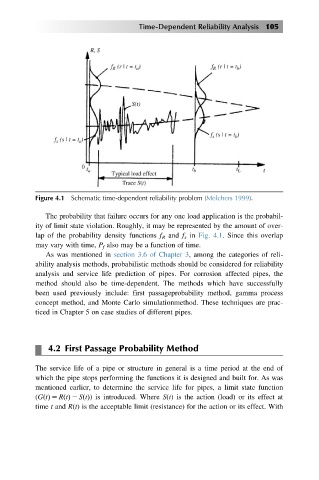
Figure 4.1 Schematic time-dependent reliability problem (Melchers 1999).

The probability that failure occurs for any one load application is the probabil-
ity of limit state violation. Roughly, it may be represented by the amount of over-
lap of the probability density functions f R and f s in Fig. 4.1. Since this overlap
may vary with time, P f also may be a function of time.
As was mentioned in section 3.6 of Chapter 3, among the categories of reli-
ability analysis methods, probabilistic methods should be considered for reliability
analysis and service life prediction of pipes. For corrosion affected pipes, the
method should also be time-dependent. The methods which have successfully
been used previously include: first passageprobability method, gamma process
concept method, and Monte Carlo simulationmethod. These techniques are prac-
ticed in Chapter 5 on case studies of different pipes.

4.2 First Passage Probability Method

The service life of a pipe or structure in general is a time period at the end of
which the pipe stops performing the functions it is designed and built for. As was
mentioned earlier, to determine the service life for pipes, a limit state function
(GtðÞ 5 RtðÞ 2 StðÞ) is introduced. Where S(t) is the action (load) or its effect at
time t and R(t) is the acceptable limit (resistance) for the action or its effect. With