Page 187 - Renewable Energy Devices and System with Simulations in MATLAB and ANSYS

174 Renewable Energy Devices and Systems with Simulations in MATLAB and ANSYS ®
®

0.30

0.25

0.20

C p 0.15
0.10
5.25
3.50
0.05
1.75 λ c
0.00 0.00
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
λ t

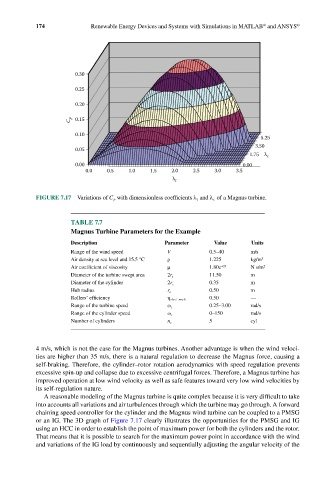
FIGURE 7.17 Variations of C p with dimensionless coefficients λ t and λ c of a Magnus turbine.

TABLE 7.7
Magnus Turbine Parameters for the Example
Description Parameter Value Units
Range of the wind speed V 0.5–40 m/s
Air density at sea level and 15.5 °C ρ 1.225 kg/m 3
Air coefficient of viscosity μ 1.80e –05 N s/m 2
Diameter of the turbine swept area 2r t 11.50 m
Diameter of the cylinder 2r c 0.35 m
Hub radius r o 0.50 m
Rollers’ efficiency η elect mech− 0.50 —
Range of the turbine speed ω t 0.25–3.00 rad/s
Range of the cylinder speed ω c 0–150 rad/s
Number of cylinders n c 5 cyl

4 m/s, which is not the case for the Magnus turbines. Another advantage is when the wind veloci-
ties are higher than 35 m/s, there is a natural regulation to decrease the Magnus force, causing a
self-braking. Therefore, the cylinder–rotor rotation aerodynamics with speed regulation prevents
excessive spin-up and collapse due to excessive centrifugal forces. Therefore, a Magnus turbine has
improved operation at low wind velocity as well as safe features toward very low wind velocities by
its self-regulation nature.
A reasonable modeling of the Magnus turbine is quite complex because it is very difficult to take
into accounts all variations and air turbulences through which the turbine may go through. A forward
chaining speed controller for the cylinder and the Magnus wind turbine can be coupled to a PMSG
or an IG. The 3D graph of Figure 7.17 clearly illustrates the opportunities for the PMSG and IG
using an HCC in order to establish the point of maximum power for both the cylinders and the rotor.
That means that it is possible to search for the maximum power point in accordance with the wind
and variations of the IG load by continuously and sequentially adjusting the angular velocity of the