Page 201 -

184 Computed-Torque Control

controller is generally found by designing a continuous-time controller, which
is then digitized using approximation techniques such as Euler’s method. That
is, for nonlinear systems, the controller discretization schemes are generally
not exact. This results in degraded performance. To verify that the controller
performance will be suitable, the simulation should provide the response at
all times, including times between the samples.
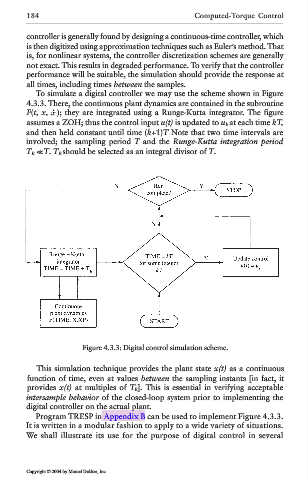
To simulate a digital controller we may use the scheme shown in Figure
4.3.3. There, the continuous plant dynamics are contained in the subroutine
F(t, x, ); they are integrated using a Runge-Kutta integrator. The figure
assumes a ZOH; thus the control input u(t) is updated to u k at each time kT,
and then held constant until time (k+1)T Note that two time intervals are
involved; the sampling period T and the Runge-Kutta integration period
T R << T. T R should be selected as an integral divisor of T.

Figure 4.3.3: Digital control simulation scheme.

This simulation technique provides the plant state x(t) as a continuous
function of time, even at values between the sampling instants [in fact, it
provides x(t) at multiples of T R ]. This is essential in verifying acceptable
intersample behavior of the closed-loop system prior to implementing the
digital controller on the actual plant.
Program TRESP in Appendix B can be used to implement Figure 4.3.3.
It is written in a modular fashion to apply to a wide variety of situations.
We shall illustrate its use for the purpose of digital control in several

Copyright © 2004 by Marcel Dekker, Inc.