Page 123 - Rock Mechanics For Underground Mining

STRENGTH CRITERIA FOR ISOTROPIC ROCK MATERIAL

r = 1 = 2 > a = 3 . With modern servocontrolled testing machines, almost any
desired total or effective stress path can be followed within the limitations imposed
by the axisymmetric configuration of the triaxial cell. Swanson and Brown (1971)
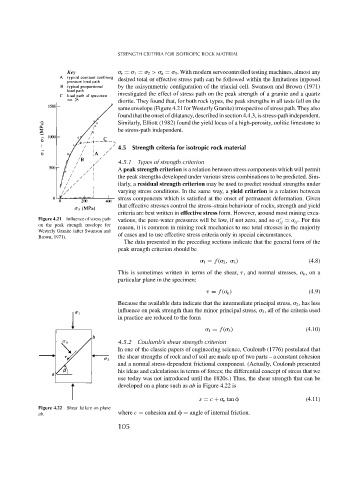
investigated the effect of stress path on the peak strength of a granite and a quartz
diorite. They found that, for both rock types, the peak strengths in all tests fell on the
same envelope (Figure 4.21 for Westerly Granite) irrespective of stress path. They also
found that the onset of dilatancy, described in section 4.4.3, is stress-path independent.
Similarly, Elliott (1982) found the yield locus of a high-porosity, oolitic limestone to
be stress-path independent.

4.5 Strength criteria for isotropic rock material

4.5.1 Types of strength criterion
A peak strength criterion is a relation between stress components which will permit
the peak strengths developed under various stress combinations to be predicted. Sim-
ilarly, a residual strength criterion may be used to predict residual strengths under
varying stress conditions. In the same way, a yield criterion is a relation between
stress components which is satisfied at the onset of permanent deformation. Given
that effective stresses control the stress–strain behaviour of rocks, strength and yield
criteria are best written in effective stress form. However, around most mining exca-
Figure 4.21 Influence of stress path vations, the pore-water pressures will be low, if not zero, and so ij . For this

ij
on the peak strength envelope for reason, it is common in mining rock mechanics to use total stresses in the majority
Westerly Granite (after Swanson and
Brown, 1971). of cases and to use effective stress criteria only in special circumstances.
The data presented in the preceding sections indicate that the general form of the
peak strength criterion should be
1 = f ( 2 , 3 ) (4.8)

This is sometimes written in terms of the shear, , and normal stresses, n ,ona
particular plane in the specimen:

= f ( n ) (4.9)
Because the available data indicate that the intermediate principal stress, 2 , has less
influence on peak strength than the minor principal stress, 3 , all of the criteria used
in practice are reduced to the form
1 = f ( 3 ) (4.10)

4.5.2 Coulomb’s shear strength criterion
In one of the classic papers of engineering science, Coulomb (1776) postulated that
the shear strengths of rock and of soil are made up of two parts – a constant cohesion
and a normal stress-dependent frictional component. (Actually, Coulomb presented
his ideas and calculations in terms of forces; the differential concept of stress that we
use today was not introduced until the 1820s.) Thus, the shear strength that can be
developed on a plane such as ab in Figure 4.22 is

s = c + n tan (4.11)
Figure 4.22 Shear failure on plane
ab. where c = cohesion and = angle of internal friction.
105