Page 401 - Rock Mechanics For Underground Mining

ELEMENTARY ANALYSIS OF PILLAR SUPPORT

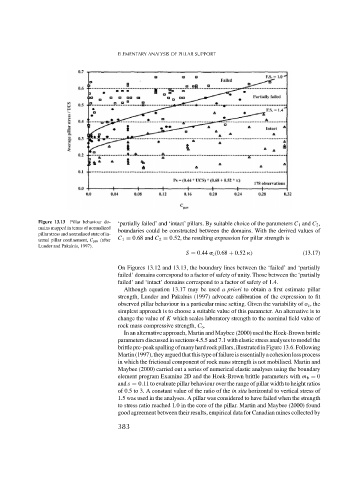
Figure 13.13 Pillar behaviour do- ‘partially failed’ and ‘intact’ pillars. By suitable choice of the parameters C 1 and C 2 ,
mains mapped in terms of normalized
pillar stress and normalised state of in- boundaries could be constructed between the domains. With the derived values of
C 1 = 0.68 and C 2 = 0.52, the resulting expression for pillar strength is
ternal pillar confinement, C pav (after
Lunder and Pakalnis, 1997).
S = 0.44 c (0.68 + 0.52 ) (13.17)

On Figures 13.12 and 13.13, the boundary lines between the ‘failed’ and ‘partially
failed’ domains correspond to a factor of safety of unity. Those between the ‘partially
failed’ and ‘intact’ domains correspond to a factor of safety of 1.4.
Although equation 13.17 may be used a priori to obtain a first estimate pillar
strength, Lunder and Pakalnis (1997) advocate calibration of the expression to fit
observed pillar behaviour in a particular mine setting. Given the variability of c , the
simplest approach is to choose a suitable value of this parameter. An alternative is to
change the value of K which scales laboratory strength to the nominal field value of
rock mass compressive strength, C o .
In an alternative approach, Martin and Maybee (2000) used the Hoek-Brown brittle
parameters discussed in sections 4.5.5 and 7.1 with elastic stress analyses to model the
brittlepre-peakspallingofmanyhardrockpillars,illustratedinFigure13.6.Following
Martin(1997),theyarguedthatthistypeoffailureisessentiallyacohesionlossprocess
in which the frictional component of rock mass strength is not mobilised. Martin and
Maybee (2000) carried out a series of numerical elastic analyses using the boundary
element program Examine 2D and the Hoek-Brown brittle parameters with m b = 0
and s = 0.11 to evaluate pillar behaviour over the range of pillar width to height ratios
of 0.5 to 3. A constant value of the ratio of the in situ horizontal to vertical stress of
1.5 was used in the analyses. A pillar was considered to have failed when the strength
to stress ratio reached 1.0 in the core of the pillar. Martin and Maybee (2000) found
good agreement between their results, empirical data for Canadian mines collected by
383