Page 139 - Satellite Communications, Fourth Edition

Polarization 119

As a caution it should be noted that the classical optics definition of
circular polarization is just the opposite of the IEEE definition. The
IEEE definition will be used throughout this text.
For a right-hand set of axes (Fig. 5.1) and with propagation along the
z axis, then when viewed along the direction of propagation (from
“behind”) and with the y axis directed upward, the x axis will be
is 0 and
directed toward the left. Consider now Eq. (5.4). At wt 0, E y
E is a maximum at E along the x axis. At wt 90°, E is zero and E y
x
x
is a maximum at E along the y axis. In other words, the resultant field
of amplitude E has rotated from the x axis to the y axis, which is a
clockwise rotation when viewed along the direction of propagation.
Equation (5.4) therefore represents RHC polarization.
Given that Eq. (5.4) represents RHC polarization, it is left as an exer-
cise to show that the following equations represent LHC polarization:

E â E sinwt (5.5a)
y
y
â E coswt (5.5b)
E x x
In the more general case, a wave may be elliptically polarized. This
occurs when the two linear components are

E â E sinwt (5.6a)
y
y
y
E â E sin(wt ) (5.6b)
x
x
x
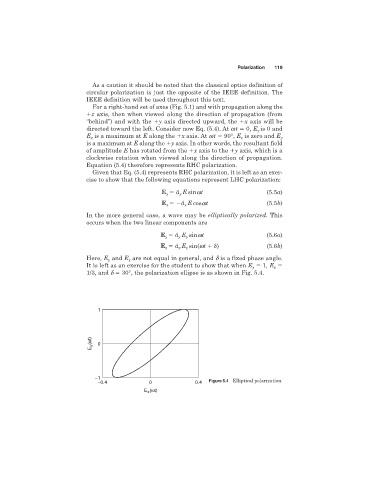
Here, E and E are not equal in general, and d is a fixed phase angle.
x
y
It is left as an exercise for the student to show that when E 1, E
x
y
1/3, and d 30°, the polarization ellipse is as shown in Fig. 5.4.
1

E y (ωt) 0

–1
–0.4 0 0.4 Figure 5.4 Elliptical polarization.
E (ωt)
x