Page 186 - Schaum's Outline of Differential Equations
P. 186
CHAP. 18] GRAPHICAL METHODS FOR SOLVING DIFFERENTIAL EQUATIONS 169
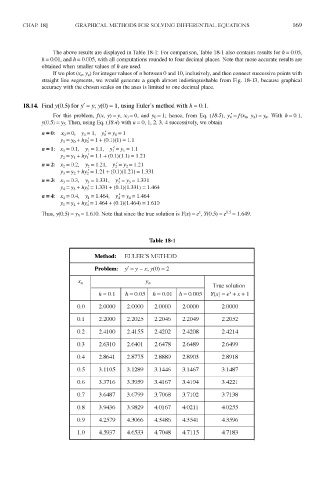
The above results are displayed in Table 18-1: For comparison, Table 18-1 also contains results for h = 0.05,
h = 0.01, and h = 0.005, with all computations rounded to four decimal places. Note that more accurate results are
obtained when smaller values of h are used.
If we plot (x n, y n) for integer values of n between 0 and 10, inclusively, and then connect successive points with
straight line segments, we would generate a graph almost indistinguishable from Fig. 18-13, because graphical
accuracy with the chosen scales on the axes is limited to one decimal place.
18.14. Find y(0.5) for / = y; y(0) = 1, using Euler's method with h = 0.1.
For this problem, (x, y)=y, x 0 = 0, and y 0= 1; hence, from Eq. (18.5), y!,=f(x n, y n)=y n. With h = 0.1,
f
y(O.S) = y s. Then, using Eq. (18.4) with n = 0, 1, 2, 3, 4 successively, we obtain
5
Thus, X0.5) = y 5 = 1.610. Note that since the true solution is Y(x) = if, 7(0.5) = e°- = 1.649.
Table 18-1
Method: EULER'S METHOD
Problem: y' = y -x; y(0) = 2
y
x n n True solution
h = 0.1 h = 0.05 ft = 0.01 h = 0.005 Y(x) = (f + x + 1
0.0 2.0000 2.0000 2.0000 2.0000 2.0000
0.1 2.2000 2.2025 2.2046 2.2049 2.2052
0.2 2.4100 2.4155 2.4202 2.4208 2.4214
0.3 2.6310 2.6401 2.6478 2.6489 2.6499
0.4 2.8641 2.8775 2.8889 2.8903 2.8918
0.5 3.1105 3.1289 3.1446 3.1467 3.1487
0.6 3.3716 3.3959 3.4167 3.4194 3.4221
0.7 3.6487 3.6799 3.7068 3.7102 3.7138
0.8 3.9436 3.9829 4.0167 4.0211 4.0255
0.9 4.2579 4.3066 4.3486 4.3541 4.3596
1.0 4.5937 4.6533 4.7048 4.7115 4.7183