Page 188 - Schaum's Outline of Differential Equations

CHAP. 18] GRAPHICAL METHODS FOR SOLVING DIFFERENTIAL EQUATIONS 171

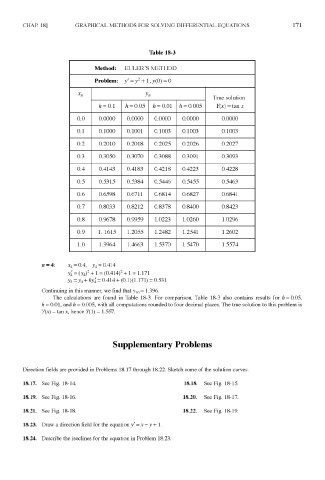
Table 18-3

Method: EULER'S METHOD
2
Problem: / = y + 1 ; y(0) = 0
y
x n n True solution
h = 0.l h = 0.05 ft = 0.01 h = 0.005 Y(x) = tan x

0.0 0.0000 0.0000 0.0000 0.0000 0.0000
0.1 0.1000 0.1001 0.1003 0.1003 0.1003

0.2 0.2010 0.2018 0.2025 0.2026 0.2027
0.3 0.3050 0.3070 0.3088 0.3091 0.3093

0.4 0.4143 0.4183 0.4218 0.4223 0.4228
0.5 0.5315 0.5384 0.5446 0.5455 0.5463

0.6 0.6598 0.6711 0.6814 0.6827 0.6841
0.7 0.8033 0.8212 0.8378 0.8400 0.8423

0.8 0.9678 0.9959 1.0223 1.0260 1.0296
0.9 1. 1615 1.2055 1.2482 1.2541 1.2602

1.0 1.3964 1.4663 1.5370 1.5470 1.5574

n = 4:

Continuing in this manner, we find that y w = 1.396.
The calculations are found in Table 18-3. For comparison, Table 18-3 also contains results for h = 0.05,
h = 0.01, and h = 0.005, with all computations rounded to four decimal places. The true solution to this problem is
Y(x) = tan x, hence 7(1) = 1.557.

Supplementary Problems

Direction fields are provided in Problems 18.17 through 18.22. Sketch some of the solution curves.
18.17. See Fig. 18-14. 18.18. See Fig. 18-15.

18.19. See Fig. 18-16. 18.20. See Fig. 18-17.

18.21. See Fig. 18-18. 18.22. See Fig. 18-19.

18.23. Draw a direction field for the equation y' = x - y + 1.
18.24. Describe the isoclines for the equation in Problem 18.23.