Page 187 - Schaum's Outline of Differential Equations

170 GRAPHICAL METHODS FOR SOLVING DIFFERENTIAL EQUATIONS [CHAP. 18

18.15. Find (l) for y' = y; y(0) = 1, using Euler's method with h = 0.1.
y
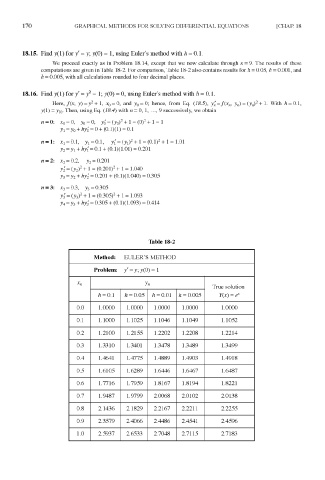
We proceed exactly as in Problem 18.14, except that we now calculate through n = 9. The results of these
computations are given in Table 18-2. For comparison, Table 18-2 also contains results for h = 0.05, h = 0.001, and
h = 0.005, with all calculations rounded to four decimal places.

18.16. Find y(l) for / = /+!; y(Q) = 0, using Euler's method with h = 0.1.
2
Here,/(*, y)=y +l, x 0 = 0, and y 0 = 0; hence, from Eq. (18.5), ?„'=/(*„, y n) = (y n) 2 + 1. With A = 0.1,
y(l) = y w. Then, using Eq. (18.4) with n = 0, 1, ..., 9 successively, we obtain

Table 18-2

Method: EULER'S METHOD

Problem: / = y; y(0) = 1
y
x n n True solution
h = 0.l h = 0.05 ft = 0.01 h = 0.005 Y(x) = f
0.0 1.0000 1.0000 1.0000 1.0000 1.0000

0.1 1.1000 1.1025 1.1046 1.1049 1.1052
0.2 1.2100 1.2155 1.2202 1.2208 1.2214

0.3 1.3310 1.3401 1.3478 1.3489 1.3499
0.4 1.4641 1.4775 1.4889 1.4903 1.4918

0.5 1.6105 1.6289 1.6446 1.6467 1.6487
0.6 1.7716 1.7959 1.8167 1.8194 1.8221

0.7 1.9487 1.9799 2.0068 2.0102 2.0138
0.8 2.1436 2.1829 2.2167 2.2211 2.2255

0.9 2.3579 2.4066 2.4486 2.4541 2.4596
1.0 2.5937 2.6533 2.7048 2.7115 2.7183