Page 224 - Schaum's Outline of Differential Equations

CHAP. 20] SOLVING SECOND-ORDER DIFFERENTIAL EQUATIONS 207

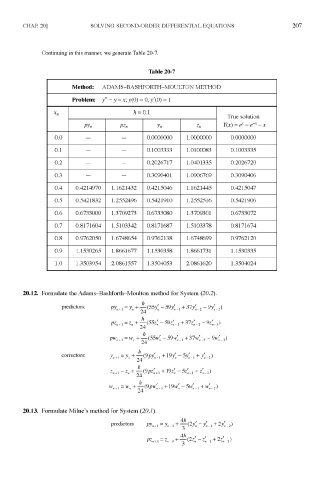
Continuing in this manner, we generate Table 20-7.

Table 20-7

Method: ADAMS-BASHFORTH-MOULTON METHOD
Problem: y"-y = x; y(0) = 0, /(O) = 1

h = 0.l
x n
True solution
x
f
py n PZ n y n •7 •^n Y(x) = e -e~ -x
0.0 — — 0.0000000 1.0000000 0.0000000
0.1 — — 0.1003333 1.0100083 0.1003335

0.2 — — 0.2026717 1.0401335 0.2026720
0.3 — — 0.3090401 1.0906769 0.3090406

0.4 0.4214970 1.1621432 0.4215046 1.1621445 0.4215047
0.5 0.5421832 1.2552496 0.5421910 1.2552516 0.5421906

0.6 0.6733000 1.3709273 0.6733080 1.3709301 0.6733072
0.7 0.8171604 1.5103342 0.8171687 1.5103378 0.8171674

0.8 0.9762050 1.6748654 0.9762138 1.6748699 0.9762120
0.9 1.1530265 1.8661677 1.1530358 1.8661731 1.1530335

1.0 1.3503954 2.0861557 1.3504053 2.0861620 1.3504024

20.12. Formulate the Adams-Bashforth-Moulton method for System (20.2).
predictors:

correctors:

20.13. Formulate Milne's method for System (20.7).

predictors: