Page 52 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 3] FUNCTIONS, LIMITS, AND CONTINUITY 43

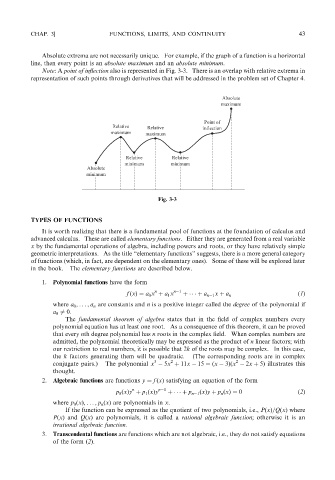
Absolute extrema are not necessarily unique. For example, if the graph of a function is a horizontal
line, then every point is an absolute maximum and an absolute minimum.
Note:A point of inflection also is represented in Fig. 3-3. There is an overlap with relative extrema in
representation of such points through derivatives that will be addressed in the problem set of Chapter 4.

Fig. 3-3

TYPES OF FUNCTIONS
It is worth realizing that there is a fundamental pool of functions at the foundation of calculus and
advanced calculus. These are called elementary functions. Either they are generated from a real variable
x by the fundamental operations of algebra, including powers and roots, or they have relatively simple
geometric interpretations. As the title ‘‘elementary functions’’ suggests, there is a more general category
of functions (which, in fact, are dependent on the elementary ones). Some of these will be explored later
in the book. The elementary functions are described below.

1. Polynomial functions have the form
n
f ðxÞ¼ a 0 x þ a 1 x n 1 þ þ a n 1 x þ a n ð1Þ
where a 0 ; ... ; a n are constants and n is a positive integer called the degree of the polynomial if
a 0 6¼ 0.
The fundamental theorem of algebra states that in the field of complex numbers every
polynomial equation has at least one root. As a consequence of this theorem, it can be proved
that every nth degree polynomial has n roots in the complex field. When complex numbers are
admitted, the polynomial theoretically may be expressed as the product of n linear factors; with
our restriction to real numbers, it is possible that 2k of the roots may be complex. In this case,
the k factors generating them will be quadratic. (The corresponding roots are in complex
2
3
2
conjugate pairs.) The polynomial x 5x þ 11x 15 ¼ðx 3Þðx 2x þ 5Þ illustrates this
thought.
2. Algebraic functions are functions y ¼ f ðxÞ satisfying an equation of the form
n
p 0 ðxÞy þ p 1 ðxÞy n 1 þ þ p n 1 ðxÞy þ p n ðxÞ¼ 0 ð2Þ
where p 0 ðxÞ; ... ; p n ðxÞ are polynomials in x.
If the function can be expressed as the quotient of two polynomials, i.e., PðxÞ=QðxÞ where
PðxÞ and QðxÞ are polynomials, it is called a rational algebraic function; otherwise it is an
irrational algebraic function.
3. Transcendental functions are functions which are not algebraic, i.e., they do not satisfy equations
of the form (2).