Page 57 - Schaum's Outline of Theory and Problems of Advanced Calculus

48 FUNCTIONS, LIMITS, AND CONTINUITY [CHAP. 3

Theorem 7. If f ðxÞ is continuous in ½a; bŠ and if f ðaÞ¼ A and f ðbÞ¼ B, then corresponding to any
number C between A and B there exists at least one number c in ½a; bŠ such that f ðcÞ¼ C. This is
sometimes called the intermediate value theorem.

Theorem 8. If f ðxÞ is continuous in ½a; bŠ and if f ðaÞ and f ðbÞ have opposite signs, there is at least one
number c for which f ðcÞ¼ 0 where a < c < b. This is related to Theorem 7.

Theorem 9. If f ðxÞ is continuous in a closed interval, then f ðxÞ has a maximum value M for at least one
value of x in the interval and a minimum value m for at least one value of x in the interval. Further-
more, f ðxÞ assumes all values between m and M for one or more values of x in the interval.

Theorem 10. If f ðxÞ is continuous in a closed interval and if M and m are respectively the least upper
bound (l.u.b.) and greatest lower bound (g.l.b.) of f ðxÞ, there exists at least one value of x in the interval
for which f ðxÞ¼ M or f ðxÞ¼ m. This is related to Theorem 9.

PIECEWISE CONTINUITY
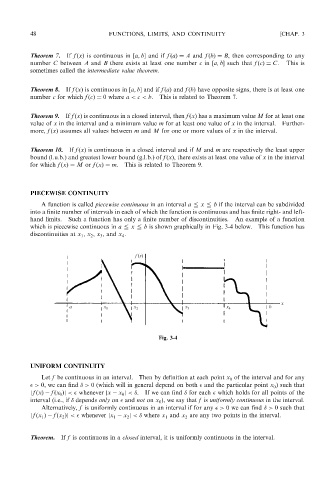
A function is called piecewise continuous in an interval a @ x @ b if the interval can be subdivided
into a finite number of intervals in each of which the function is continuous and has finite right- and left-
hand limits. Such a function has only a finite number of discontinuities. An example of a function
which is piecewise continuous in a @ x @ b is shown graphically in Fig. 3-4 below. This function has
discontinuities at x 1 , x 2 , x 3 , and x 4 .

f (x)

x
a x 1 x 2 x 3 x 4 b

Fig. 3-4

UNIFORM CONTINUITY
Let f be continuous in an interval. Then by definition at each point x 0 of the interval and for any
> 0, we can find > 0 (which will in general depend on both and the particular point x 0 ) such that
j f ðxÞ f ðx 0 Þj < whenever jx x 0 j < . If we can find for each which holds for all points of the
interval (i.e., if depends only on and not on x 0 ), we say that f is uniformly continuous in the interval.
Alternatively, f is uniformly continuous in an interval if for any > 0we can find > 0 such that
j f ðx 1 Þ f ðx 2 Þj < whenever jx 1 x 2 j < where x 1 and x 2 are any two points in the interval.

Theorem. If f is continuous in a closed interval, it is uniformly continuous in the interval.