Page 58 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 3] FUNCTIONS, LIMITS, AND CONTINUITY 49

Solved Problems

FUNCTIONS

3.1. Let f ðxÞ¼ ðx 2Þð8 xÞ for 2 @ x @ 8. (a) Find f ð6Þ and f ð 1Þ.(b) What is the domain of
definition of f ðxÞ? (c) Find f ð1 2tÞ and give the domain of definition. (d) Find f ½ f ð3ފ,
f ½ f ð5ފ. (e) Graph f ðxÞ.

(a) f ð6Þ¼ð6 2Þð8 6Þ¼ 4 2 ¼ 8
f ð 1Þ is not defined since f ðxÞ is defined only for 2 @ x @ 8.
(b) The set of all x such that 2 @ x @ 8.
(c) f ð1 2tÞ¼ fð1 2tÞ 2gf8 ð1 2tÞg ¼ ð1 þ 2tÞð7 þ 2tÞ where t is such that 2 @ 1 2t @ 8, i.e.,
7=2 @ t @ 1=2.
(d) f ð3Þ¼ð3 2Þð8 3Þ¼ 5, f (x)
f ½ f ð3ފ ¼ f ð5Þ¼ð5 2Þð8 5Þ¼ 9.
f ð5Þ¼ 9so that f ½ f ð5ފ ¼ f ð9Þ is not defined. 8
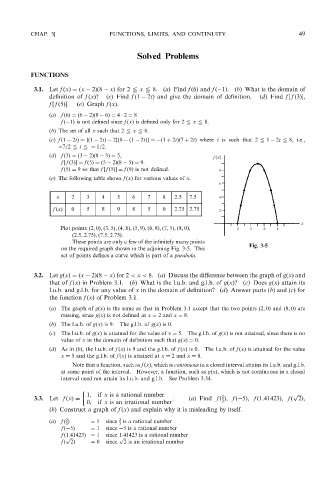
(e) The following table shows f ðxÞ for various values of x.
6
x 2 3 4 5 6 7 8 2.5 7.5 4
0 5 8 9 8 5 0 2.75 2.75
f ðxÞ 2
x
Plot points ð2; 0Þ; ð3; 5Þ; ð4; 8Þ; ð5; 9Þ; ð6; 8Þ; ð7; 5Þ; ð8; 0Þ; 2 4 6 8
ð2:5; 2:75Þ; ð7:5; 2:75Þ.
These points are only a few of the infinitely many points
Fig. 3-5
on the required graph shown in the adjoining Fig. 3-5. This
set of points defines a curve which is part of a parabola.

3.2. Let gðxÞ¼ðx 2Þð8 xÞ for 2 < x < 8. (a) Discuss the difference between the graph of gðxÞ and
that of f ðxÞ in Problem 3.1. (b) What is the l.u.b. and g.l.b. of gðxÞ? (c) Does gðxÞ attain its
l.u.b. and g.l.b. for any value of x in the domain of definition? (d) Answer parts (b) and (c) for
the function f ðxÞ of Problem 3.1.
(a) The graph of gðxÞ is the same as that in Problem 3.1 except that the two points ð2; 0Þ and ð8; 0Þ are
missing, since gðxÞ is not defined at x ¼ 2 and x ¼ 8.
(b) The l.u.b. of gðxÞ is 9. The g.l.b. of gðxÞ is 0.
(c) The l.u.b. of gðxÞ is attained for the value of x ¼ 5. The g.l.b. of gðxÞ is not attained, since there is no
value of x in the domain of definition such that gðxÞ¼ 0.
(d)As in (b), the l.u.b. of f ðxÞ is 9 and the g.l.b. of f ðxÞ is 0. The l.u.b. of f ðxÞ is attained for the value
x ¼ 5 and the g.l.b. of f ðxÞ is attained at x ¼ 2 and x ¼ 8.
Note that a function, such as f ðxÞ, which is continuous in a closed interval attains its l.u.b. and g.l.b.
at some point of the interval. However, a function, such as gðxÞ, which is not continuous in a closed
interval need not attain its l.u.b. and g.l.b. See Problem 3.34.

1; if x is a rational number 2 p ffiffiffi
3
0; if x is an irrational number
3.3. Let f ðxÞ¼ . (a) Find f ð Þ, f ð 5Þ, f ð1:41423Þ, f ð 2Þ,
(b) Construct a graph of f ðxÞ and explain why it is misleading by itself.
2 2
3
(a) f ð Þ ¼ 1 since 3 is a rational number
¼ 1 since 5isa rational number
f ð 5Þ
f ð1:41423Þ¼ 1 since 1.41423 is a rational number
p ffiffiffi p ffiffiffi
¼ 0 since 2 is an irrational number
f ð 2Þ