Page 60 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 3] FUNCTIONS, LIMITS, AND CONTINUITY 51

f (x)
y = x f (x)

1/2p 1/p
x
x
_ 3 _ 2 _ 1 1 2 3 4 5
y = _
x

Fig. 3-8 Fig. 3-9

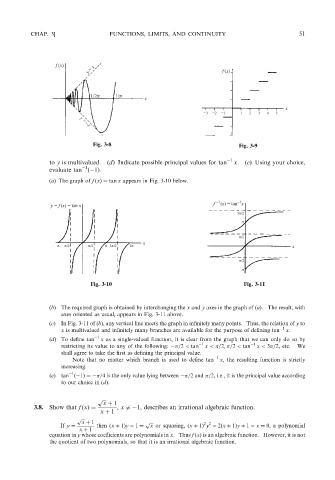
to y is multivalued. (d) Indicate possible principal values for tan 1 x.(e) Using your choice,
1
evaluate tan ð 1Þ.
(a) The graph of f ðxÞ¼ tan x appears in Fig. 3-10 below.

_ 1 _ 1
y = f (x) = tan x f (x) = tan x
3p/2
p

p/2
_ p _ p/2 p/2 p 3p/2 2p x x

_
p/2
_ p
Fig. 3-10 Fig. 3-11

(b) The required graph is obtained by interchanging the x and y axes in the graph of (a). The result, with
axes oriented as usual, appears in Fig. 3-11 above.
(c) In Fig. 3-11 of (b), any vertical line meets the graph in infinitely many points. Thus, the relation of y to
x is multivalued and infinitely many branches are available for the purpose of defining tan 1 x.
(d)To define tan 1 x as a single-valued function, it is clear from the graph that we can only do so by
restricting its value to any of the following: =2 < tan 1 x < =2; =2 < tan 1 x < 3 =2, etc. We
shall agree to take the first as defining the principal value.
Note that no matter which branch is used to define tan 1 x,the resulting function is strictly
increasing.
1
(e) tan ð 1Þ¼ =4isthe only value lying between =2 and =2, i.e., it is the principal value according
to our choice in ðdÞ.

ffiffiffi
p
x þ 1
, x 6¼ 1, describes an irrational algebraic function.
3.8. Show that f ðxÞ¼
x þ 1
p ffiffiffi
x þ 1 p ffiffiffi 2 2
x or squaring, ðx þ 1Þ y 2ðx þ 1Þy þ 1 x ¼ 0, a polynomial
If y ¼ then ðx þ 1Þy 1 ¼
x þ 1
equation in y whose coefficients are polynomials in x. Thus f ðxÞ is an algebraic function. However, it is not
the quotient of two polynomials, so that it is an irrational algebraic function.