Page 77 - Schaum's Outline of Theory and Problems of Advanced Calculus

68 DERIVATIVES [CHAP. 4

Because of the definitions (8) and (10),we often write
dy f ðx þ xÞ f ðxÞ y
¼ f ðxÞ¼ lim ¼ lim
0
dx x!0 x x!0 x ð11Þ
It is emphasized that dx and dy are not the limits of x and y as x ! 0, since these limits are zero
whereas dx and dy are not necessarily zero. Instead, given dx we determine dy from (10), i.e., dy is a
dependent variable determined from the independent variable dx for a given x.
Geometrically, dy is represented in Fig. 4-1, for the particular value x ¼ x 0 ,by the line segment SR,
whereas y is represented by QR.
The geometric interpretation of the derivative as the slope of the tangent line to a curve at one of its
points is fundamental to its application. Also of importance is its use as representative of instantaneous
velocity in the construction of physical models. In particular, this physical viewpoint may be used to
introduce the notion of differentials.
Newton’s Second and First Laws of Motion imply that the path of an object is determined by the
forces acting on it, and that if those forces suddenly disappear, the object takes on the tangential
direction of the path at the point of release. Thus, the nature of the path in a small neighborhood
of the point of release becomes of interest. With this thought in mind, consider the following idea.
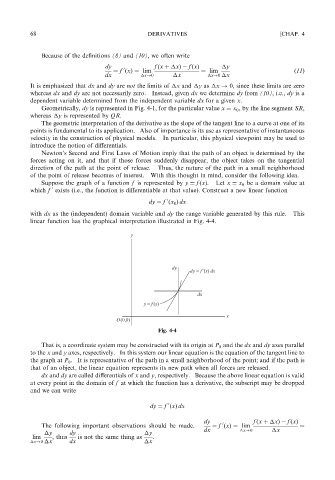
Suppose the graph of a function f is represented by y ¼ f ðxÞ. Let x ¼ x 0 be a domain value at
which f exists (i.e., the function is differentiable at that value). Construct a new linear function
0
dy ¼ f ðx 0 Þ dx
0
with dx as the (independent) domain variable and dy the range variable generated by this rule. This
linear function has the graphical interpretation illustrated in Fig. 4-4.

Fig. 4-4

That is, a coordinate system may be constructed with its origin at P 0 and the dx and dy axes parallel
to the x and y axes, respectively. In this system our linear equation is the equation of the tangent line to
the graph at P 0 .Itis representative of the path in a small neighborhood of the point; and if the path is
that of an object, the linear equation represents its new path when all forces are released.
dx and dy are called differentials of x and y, respectively. Because the above linear equation is valid
at every point in the domain of f at which the function has a derivative, the subscript may be dropped
and we can write

dy ¼ f ðxÞ dx
0
dy
The following important observations should be made. ¼ f ðxÞ¼ lim f ðx þ xÞ f ðxÞ ¼
0
y dy y dx x!0 x
lim , thus is not the same thing as .
x!0 x dx x