Page 75 - Schaum's Outline of Theory and Problems of Advanced Calculus

66 DERIVATIVES [CHAP. 4

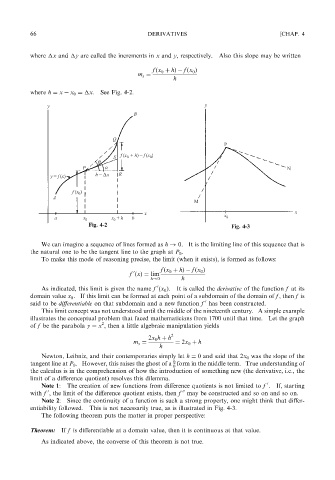
where x and y are called the increments in x and y, respectively. Also this slope may be written

f ðx 0 þ hÞ f ðx 0 Þ
h
m s ¼
where h ¼ x x 0 ¼ x. See Fig. 4-2.

y y
B

Q
P
_
f (x 0 + h) f (x 0 )
S
θ
P α N
h = Dx R
y = f (x)
f (x 0 )
A
M
x x
a x 0 x 0 + h b x 0
Fig. 4-2 Fig. 4-3

We can imagine a sequence of lines formed as h ! 0. It is the limiting line of this sequence that is
the natural one to be the tangent line to the graph at P 0 .
To make this mode of reasoning precise, the limit (when it exists), is formed as follows:
f ðxÞ¼ lim f ðx 0 þ hÞ f ðx 0 Þ
0
h!0 h
As indicated, this limit is given the name f ðx 0 Þ. Itis called the derivative of the function f at its
0
domain value x 0 .If this limit can be formed at each point of a subdomain of the domain of f , then f is
said to be differentiable on that subdomain and a new function f has been constructed.
0
This limit concept was not understood until the middle of the nineteenth century. A simple example
illustrates the conceptual problem that faced mathematicians from 1700 until that time. Let the graph
2
of f be the parabola y ¼ x , then a little algebraic manipulation yields
2x 0 h þ h 2
¼ 2x 0 þ h
h
m s ¼
Newton, Leibniz, and their contemporaries simply let h ¼ 0 and said that 2x 0 was the slope of the
0
tangent line at P 0 . However, this raises the ghost of a form in the middle term. True understanding of
0
the calculus is in the comprehension of how the introduction of something new (the derivative, i.e., the
limit of a difference quotient) resolves this dilemma.
Note 1: The creation of new functions from difference quotients is not limited to f . If, starting
0
with f , the limit of the difference quotient exists, then f 00 may be constructed and so on and so on.
0
Note 2: Since the continuity of a function is such a strong property, one might think that differ-
entiability followed. This is not necessarily true, as is illustrated in Fig. 4-3.
The following theorem puts the matter in proper perspective:
Theorem: If f is differentiable at a domain value, then it is continuous at that value.
As indicated above, the converse of this theorem is not true.