Page 136 - Schaum's Outline of Theory and Problems of Electric Circuits

WAVEFORMS AND SIGNALS
CHAP. 6]
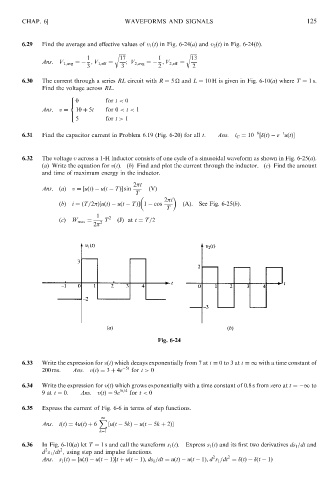
6.29 Find the average and effective values of v 1 ðtÞ in Fig. 6-24(a) and v 2 ðtÞ in Fig. 6-24(b). 125
r ffiffiffiffiffi r ffiffiffiffiffi
1 17 1 13
Ans: V 1;avg ¼ ; V 1;eff ¼ ; V 2;avg ¼ ; V 2;eff ¼
3 3 2 2
6.30 The current through a series RL circuit with R ¼ 5
and L ¼ 10 H is given in Fig. 6-10(a) where T ¼ 1s.
Find the voltage across RL.
8
> 0 for t < 0
<
Ans: v ¼ 10 þ 5t for 0 < t < 1
>
:
5 for t > 1
6
t
6.31 Find the capacitor current in Problem 6.19 (Fig. 6-20) for all t. Ans: i C ¼ 10 ½ ðtÞ e uðtފ

6.32 The voltage v across a 1-H inductor consists of one cycle of a sinusoidal waveform as shown in Fig. 6-25(a).
(a) Write the equation for vðtÞ.(b) Find and plot the current through the inductor. (c) Find the amount
and time of maximum energy in the inductor.

2 t
Ans: ðaÞ v ¼½uðtÞ uðt Tފ sin ðVÞ
T

2 t
ðbÞ i ¼ðT=2 Þ½uðtÞ uðt Tފ 1 cos ðAÞ: See Fig. 6-25ðbÞ:
T
1
ðcÞ W max ¼ T 2 ðJÞ at t ¼ T=2
2 2

Fig. 6-24

6.33 Write the expression for vðtÞ which decays exponentially from 7 at t ¼ 0to 3at t ¼1 with a time constant of
200 ms. Ans: vðtÞ¼ 3 þ 4e 5t for t > 0

6.34 Write the expression for vðtÞ which grows exponentially with a time constant of 0.8 s from zero at t ¼ 1 to
9at t ¼ 0. Ans: vðtÞ¼ 9e 5t=4 for t < 0

6.35 Express the current of Fig. 6-6 in terms of step functions.
X
1
Ans: iðtÞ¼ 4uðtÞþ 6 ½uðt 5kÞ uðt 5k þ 2ފ
k¼1
6.36 In Fig. 6-10(a) let T ¼ 1 s and call the waveform s 1 ðtÞ. Express s 1 ðtÞ and its first two derivatives ds 1 =dt and
2
2
d s 1 =dt , using step and impulse functions.
2
2
Ans: s 1 ðtÞ¼ ½uðtÞ uðt 1ފt þ uðt 1Þ; ds 1 =dt ¼ uðtÞ uðt 1Þ; d s 1 =dt ¼ ðtÞ ðt 1Þ