Page 135 - Schaum's Outline of Theory and Problems of Electric Circuits

WAVEFORMS AND SIGNALS
124
Table 6-3 [CHAP. 6
Time v i C ¼ Cdv=dt i R ¼ v=R i ¼ i C þ i R
at at at at
t < 0 v ¼ V 0 e i C ¼ CV 0 ae i R ¼ðV 0 =RÞe i ¼ v 0 ðCa þ 1=RÞe
(a) t > 0 v ¼ V 0 e at i C ¼ CV 0 ae at i R ¼ðV 0 =RÞe at i ¼ V 0 ð Ca þ 1=RÞe at
5 t
5 t
5 t
t < 0 v ¼ 10e t i C ¼ 10 e i R ¼ 10 e i ¼ 2ð10 e Þ
5 t
5 t
(b) t > 0 v ¼ 10e t i C ¼ 10 e i R ¼ 10 e i ¼ 0

Supplementary Problems

6.22 Let v 1 ¼ 8 sin 100 t and v 2 ¼ 6 sin 99 t. Show that v ¼ v 1 þ v 2 is periodic. Find the period, and the
ffiffiffi
p
maximum, average, and effective values of v. Ans: T ¼ 2; V max ¼ 14; V avg ¼ 0; V eff ¼ 5 2
6.23 Find period, frequency, phase angle in degrees, and maximum, minimum, average, and effective values of
vðtÞ¼ 2 þ 6 cos ð10 t þ =6Þ. p ffiffiffiffiffi
Ans: T ¼ 0:2s; f ¼ 5Hz; phase ¼ 308; V max ¼ 8; V min ¼ 4; V avg ¼ 2; V eff ¼ 22

6.24 Reduce vðtÞ¼ 2 cos ð!t þ 308Þþ 3 cos !t to vðtÞ¼ A sin ð!t þ Þ. Ans: A ¼ 4:84; ¼ 1028

6.25 Find V 2;avg and V 2;eff in the graph of Fig. 6-1(b) for V 1 ¼ V 2 ¼ 3, and T ¼ 4T 1 =3.
Ans: V 2;avg ¼ 1:5; V 2;eff ¼ 3
p ffiffiffi
6.26 Repeat Problem 6.25 for V 1 ¼ 0, V 2 ¼ 4, and T ¼ 2T 1 . Ans: V 2;avg ¼ 2; V 2;eff ¼ 2 2

6.27 Find V 3;avg and V 3;eff in the graph of Fig. 6-1(c) for V 0 ¼ 2 and T ¼ 200T 1 .
Ans: V 3;avg ¼ 0; V 3;eff ¼ 0:1

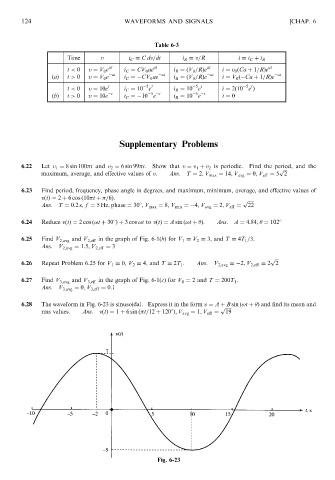
6.28 The waveform in Fig. 6-23 is sinusoidal. Express it in the form v ¼ A þ B sin ð!t þ Þ and find its mean and
ffiffiffiffiffi
p
rms values. Ans: vðtÞ¼ 1 þ 6 sin ð t=12 þ 1208Þ; V avg ¼ 1; V eff ¼ 19

Fig. 6-23