Page 144 - Schaum's Outline of Theory and Problems of Electric Circuits

FIRST-ORDER CIRCUITS
CHAP. 7]

Fig. 7-8 133

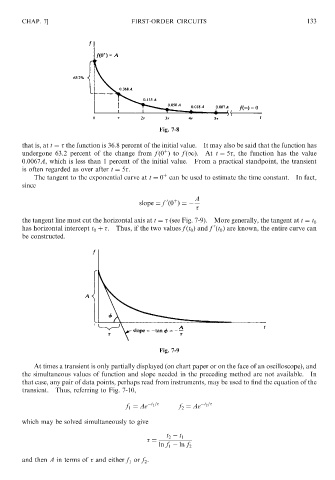
that is, at t ¼ the function is 36.8 percent of the initial value. It may also be said that the function has
þ
undergone 63.2 percent of the change from f ð0 Þ to f ð1Þ. At t ¼ 5 , the function has the value
0.0067A, which is less than 1 percent of the initial value. From a practical standpoint, the transient
is often regarded as over after t ¼ 5 .
þ
The tangent to the exponential curve at t ¼ 0 can be used to estimate the time constant. In fact,
since
A
0 þ
slope ¼ f ð0 Þ¼

the tangent line must cut the horizontal axis at t ¼ (see Fig. 7-9). More generally, the tangent at t ¼ t 0
0
has horizontal intercept t 0 þ . Thus, if the two values f ðt 0 Þ and f ðt 0 Þ are known, the entire curve can
be constructed.

Fig. 7-9

At times a transient is only partially displayed (on chart paper or on the face of an oscilloscope), and
the simultaneous values of function and slope needed in the preceding method are not available. In
that case, any pair of data points, perhaps read from instruments, may be used to find the equation of the
transient. Thus, referring to Fig. 7-10,

f ¼ Ae t 1 = f ¼ Ae t 2 =
2
1
which may be solved simultaneously to give

t 2 t 1
¼
ln f 1 ln f 2
and then A in terms of and either f 1 or f 2 .