Page 145 - Schaum's Outline of Theory and Problems of Electric Circuits

FIRST-ORDER CIRCUITS
134

Fig. 7-10 [CHAP. 7

7.7 COMPLEX FIRST-ORDER RL AND RC CIRCUITS
A more complex circuit containing resistors, sources, and a single energy storage element may be
converted to a The ´ venin or Norton equivalent as seen from the two terminals of the inductor or
capacitor. This reduces the complex circuit to a simple RC or RL circuit which may be solved accord-
ing to the methods described in the previous sections.
If a source in the circuit is suddently switched to a dc value, the resulting currents and voltages are
exponentials, sharing the same time constant with possibly different initial and final values. The time
constant of the circuit is either RC or L=R, where R is the resistance in the The ´ venin equivalent of the
circuit as seen by the capacitor or inductor.

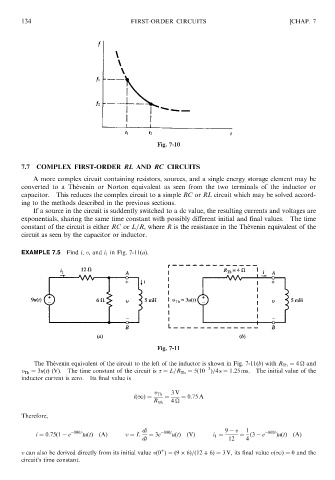
EXAMPLE 7.5 Find i, v, and i 1 in Fig. 7-11(a).

Fig. 7-11

The The ´ venin equivalent of the circuit to the left of the inductor is shown in Fig. 7-11(b) with R Th ¼ 4
and
3
v Th ¼ 3uðtÞ (V). The time constant of the circuit is ¼ L=R Th ¼ 5ð10 Þ=4s ¼ 1:25 ms. The initial value of the
inductor current is zero. Its final value is
3V
v Th
ið1Þ ¼ ¼ ¼ 0:75 A
R Th 4
Therefore,

di 800t 9 v 1 800t
800t
i ¼ 0:75ð1 e ÞuðtÞ ðAÞ v ¼ L ¼ 3e uðtÞ ðVÞ i 1 ¼ ¼ ð3 e ÞuðtÞðAÞ
dt 12 4
þ
v can also be derived directly from its initial value vð0 Þ¼ ð9 6Þ=ð12 þ 6Þ¼ 3 V, its final value vð1Þ ¼ 0 and the
circuit’s time constant.