Page 173 - Schaum's Outline of Theory and Problems of Electric Circuits

HIGHER-ORDER CIRCUITS AND COMPLEX FREQUENCY
162

Fig. 8-2 [CHAP. 8

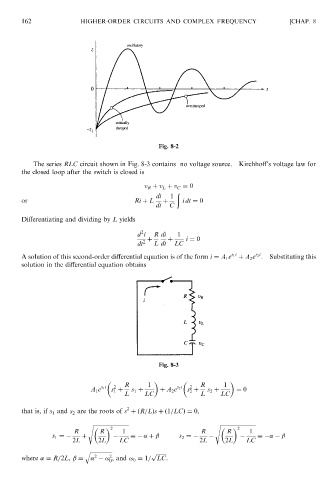
The series RLC circuit shown in Fig. 8-3 contains no voltage source. Kirchhoff’s voltage law for
the closed loop after the switch is closed is

v þ v þ v ¼ 0
L
C
R
ð
di 1
or Ri þ L þ idt ¼ 0
dt C
Differentiating and dividing by L yields
2
d i R di 1
þ þ i ¼ 0
dt 2 L dt LC
s 1 t s 2 t
A solution of this second-order differential equation is of the form i ¼ A 1 e þ A 2 e . Substituting this
solution in the differential equation obtains

Fig. 8-3

R 1 s 2 t 2 R 1
s 1 t
2
A 1 e s 1 þ s 1 þ þ A 2 e s 2 þ s 2 þ ¼ 0
L LC L LC
2
that is, if s 1 and s 2 are the roots of s þðR=LÞs þð1=LCÞ¼ 0,
s ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi s ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi

R R 2 1 R R 2 1
s 1 ¼ þ þ s 2 ¼
2L 2L LC 2L 2L LC
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi p ffiffiffiffiffiffiffi
2
2
where R=2L, ! , and ! 0 1= LC.
0