Page 177 - Schaum's Outline of Theory and Problems of Electric Circuits

HIGHER-ORDER CIRCUITS AND COMPLEX FREQUENCY
166
2
2
Since >! 0 , the circuit is overdamped and from (2) we have [CHAP. 8
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
2
2
s 1 ¼ þ ! ¼ 1271 and s 2 ¼ ! ¼ 4717
0
0

dv
At t ¼ 0; V 0 ¼ A 1 þ A 2 and ¼ s 1 A 1 þ s 2 A 2
dt t¼0
From the nodal equation (1), at t ¼ 0 and with no initial current in the inductance L,

dv dv
V 0 V 0
þ C ¼ 0 or ¼

R dt dt t¼0 RC
Solving for A 1 ,
V 0 ðs 2 þ 1=RCÞ
A 1 ¼ ¼ 155:3 and A 1 ¼ V 0 A 1 ¼ 50:0 155:3 ¼ 105:3
s 2 s 1
Substituting into (2)
1271t 4717t
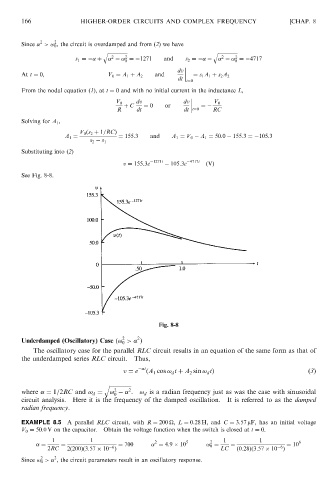
v ¼ 155:3e 105:3e ðVÞ
See Fig. 8-8.

Fig. 8-8
2 2
Underdamped (Oscillatory) Case ð! 0 > Þ
The oscillatory case for the parallel RLC circuit results in an equation of the same form as that of
the underdamped series RLC circuit. Thus,
t
v ¼ e ðA 1 cos ! d t þ A 2 sin ! d tÞ ð3Þ
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
where ¼ 1=2RC and ! d ¼ ! . ! d is a radian frequency just as was the case with sinusoidal
0
circuit analysis. Here it is the frequency of the damped oscillation. It is referred to as the damped
radian frequency.
EXAMPLE 8.5 A parallel RLC circuit, with R ¼ 200
, L ¼ 0:28 H, and C ¼ 3:57 mF, has an initial voltage
V 0 ¼ 50:0 V on the capacitor. Obtain the voltage function when the switch is closed at t ¼ 0.
1 1 1 1
2
2
¼ ¼ ¼ 700 ¼ 4:9 10 5 ! 0 ¼ ¼ ¼ 10 6
6
6
2RC 2ð200Þð3:57 10 Þ LC ð0:28Þð3:57 10 Þ
2
2
Since ! 0 > , the circuit parameters result in an oscillatory response.