Page 119 - Schaum's Outline of Theory and Problems of Signals and Systems

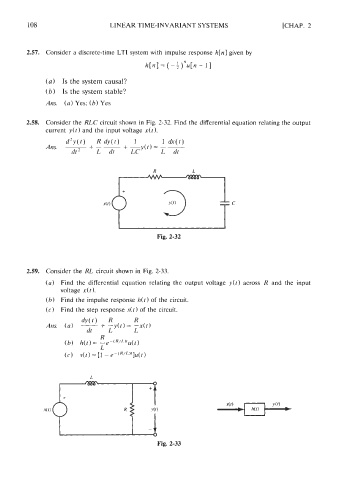
108 LINEAR TIME-INVARIANT SYSTEMS [CHAP. 2

2.57. Consider a discrete-time LTI system with impulse response h[n] given by
h[n] = (-;)l1u[n - I]

(a) Is the system causal?
(b) Is the system stable?

Ans. (a) Yes; (b) Yes

2.58. Consider the RLC circuit shown in Fig. 2-32. Find the differential equation relating the output
current y(t) and the input voltage x(t).
d2y(t) R dy(t) 1 1 &([I
Ans. --- +-- + -y(t) = - -
dt' L dt LC L dl

Fig. 2-32

2.59. Consider the RL circuit shown in Fig. 2-33.

Find the differential equation relating the output voltage y(t) across R and the input
voltage x( t 1.
Find the impulse response h(t) of the circuit.
Find the step response dt) of the circuit.

Fig. 2-33