Page 120 - Schaum's Outline of Theory and Problems of Signals and Systems

CHAP. 21 LINEAR TIME-INVARIANT SYSTEMS

2.60. Consider the system in Prob. 2.20. Find the output y(t) if x(t) = e-"'u(t) and y(0) = 0.
Am. te-"u(t)

2.61. Is the system described by the differential equation

linear?
Am. No, it is nonlinear

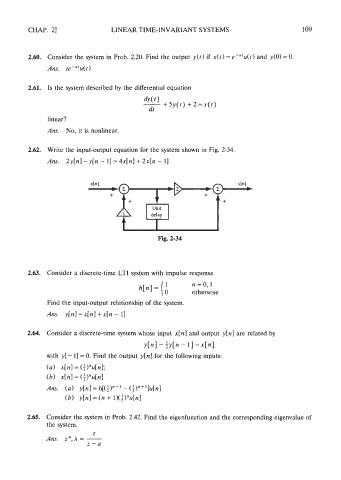
2.62. Write the input-output equation for the system shown in Fig. 2-34.
Am. 2y[n] - y[n - 11 = 4x[n] + 2x[n - 11

Fig. 2-34

2.63. Consider a discrete-time LTI system with impulse response

h[n] = n=0,1
otherwise
Find the input-output relationship of the system.

Am. y[n] = x[n] + x[n - 11

2.64. Consider a discrete-time system whose input x[n] and output y[n] are related by

y[n] - iy[n - 11 =x[n]
with y[- l] = 0. Find the output y[n] for the following inputs:
(a) x[nl = (f )"u[nl;
(b) xtnl= (f )"u[nl
Am. (a) y[n] = 6[(;)"+' - (f)"+']u[n]
(b) y[nl= (n + lX;)"u[n]

2.65. Consider the system in Prob. 2.42. Find the eigenfunction and the corresponding eigenvalue of
the system.
z
Am zn,A = -
z-a