Page 194 - Schaum's Outline of Theory and Problems of Signals and Systems

CHAP. 41 THE Z-TRANSFORM AND DISCRETE-TIME LTI SYSTEMS

(c) FromTable4-1

We see that the ROCs in Eqs. (4.64) and (4.65) do not overlap and that there is no
common ROC, and thus x[n] will not have X(z).

4.7. Let

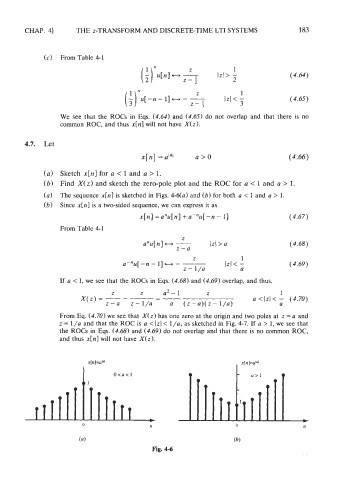
(a) Sketch x[n] for a < 1 and a > 1.
(b) Find X(z) and sketch the zero-pole plot and the ROC for a < 1 and a > 1.

(a) The sequence x[n] is sketched in Figs. 44a) and (b) for both a < 1 and a > 1.
(b) Since x[n] is a two-sided sequence, we can express it as

= anu[n] + amnu[-n - 11
~[n] (4.67)
From Table 4-1

If a < 1, we see that the ROCs in Eqs. (4.68) and (4.69) overlap, and thus,

z z a2- 1 z 1
-
-
--
X(z) = - - a < lzl < - (4.70)
z-a z-l/a a (z -a)(z- l/a) a
From Eq. (4.70) we see that X(z) has one zero at the origin and two poles at z =a and
z = l/a and that the ROC is a < lzl< l/a, as sketched in Fig. 4-7. If a > 1, we see that
the ROCs in Eqs. (4.68) and (4.69) do not overlap and that there is no common ROC,
and thus x[n] will not have X(z).

(4
Fig. 4-6