Page 259 - Schaum's Outline of Theory and Problems of Signals and Systems

248 FOURIER ANALYSIS OF TIME SIGNALS AND SYSTEMS [CHAP. 5

Hence, we obtain
sin oa sin ma
pu(t) -2- =2a-
o wa
The Fourier transform X(o) of x(t) is sketched in Fig. 5-16(b).

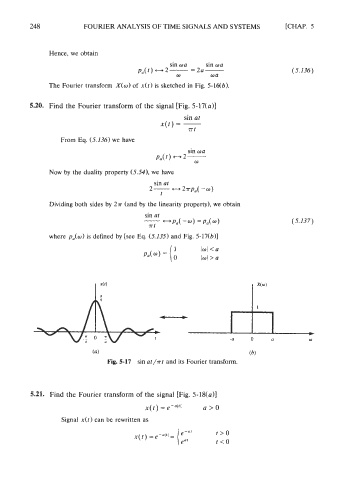
5.20. Find the Fourier transform of the signal [Fig. 5-17(a)]

sin at
x(t) = -
7Tt
From Eq. (5.136) we have
sin oa
pa(!) t-, 2-
W
Now by the duality property (5.541, we have
sin at
2- - 257pa( -o)
I
Dividing both sides by 2~ (and by the linearity property), we obtain
sin at
- -pa(-o) = pa(w)
Tt

where pa(w) is defined by [see Eq. (5.135) and Fig. 5-1Xb)I

(a) (b)
Fig. 5-17 sin at/~t and its Fourier transform.

5.21. Find the Fourier transform of the signal [Fig. 5-18(a)]

x(t) = e-alfl a>O
Signal x(t) can be rewritten as