Page 264 - Schaum's Outline of Theory and Problems of Signals and Systems

CHAP. 51 FOURIER ANALYSIS OF TIME SIGNALS AND SYSTEMS

In a similar manner we have

1 1
and Y[x(t) sin w,t] = Y -x(t) eJ"ot - - ( t ) e -'"o' I
x
[ 2i
1 1
= -X(w - w,) - -X(w + w,)
2J 2 J
Hence,

x(t) sin wot t* - j[i~(w - wo) - ;X(O + wo)]

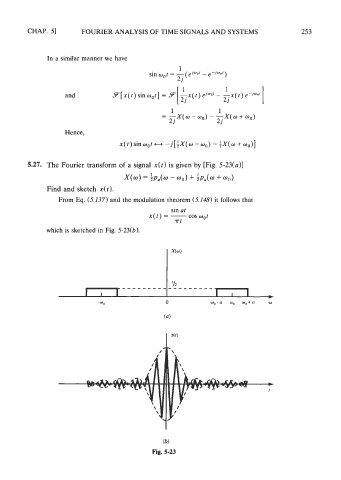
5.27. The Fourier transform of a signal x(t) is given by [Fig. 5-23(a)]

X(w) = $pa(w - wo) + ;P~(W + ~ 0 )
Find and sketch x(r).
From Eq. (5.137) and the modulation theorem (5.148) it follows that
sin at
x(t) = - COS wot
T f
which is sketched in Fig. 5-23(b).

(4
Fig. 5-23