Page 261 - Schaum's Outline of Theory and Problems of Signals and Systems

FOURIER ANALYSIS OF TIME SIGNALS AND SYSTEMS [CHAP. 5

Dividing both sides by 2a, we obtain

The Fourier transform X(w) of x(t) is shown in Fig. 5-19(b).

5.23. Find the Fourier transforms of the following signals:
(a) x(t) = 1 (b) x(t) =eJWO'
(c) x(t)=e-JWu' (d) x(t) = cos o,t
(e) x(t)=sino,t

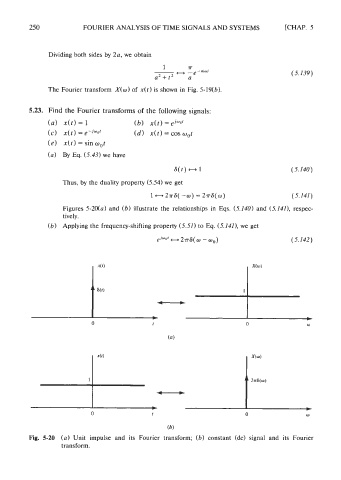
(a) By Eq. (5.43) we have

Thus, by the duality property (5.54) we get

Figures 5-20(a) and (b) illustrate the relationships in Eqs. (5.140) and (5.140, respec-
tively.
(b) Applying the frequency-shifting property (5.51) to Eq. (5.1411, we get

Fig. 5-20 (a) Unit impulse and its Fourier transform; (6) constant (dc) signal and its Fourier
transform.